
题目列表(包括答案和解析)
3.使学生系统掌握解等差数列与等比数列综合题的规律,深化数学思想方法在解题实践中的指导作用,灵活地运用数列知识和方法解决数学和实际生活中的有关问题;
2.能熟练地求一些特殊数列的通项和前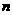 项的和;
项的和;
1. 能灵活地运用等差数列、等比数列的定义、性质、通项公式、前n项和公式解题;
23、已知曲线 ,过
,过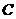 上的点
上的点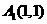 作曲线
作曲线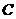 的切线
的切线 交
交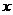 轴于点
轴于点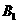 ,再过点
,再过点 作
作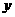 轴的平行线交曲线
轴的平行线交曲线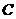 于点
于点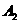 ,再过点
,再过点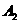 作曲线
作曲线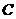 的切线
的切线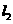 交
交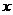 轴于点
轴于点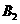 ,再过点
,再过点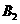 作
作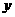 轴的平行线交曲线
轴的平行线交曲线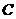 于点
于点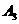 ,……,依次作下去,记点
,……,依次作下去,记点 的横坐标为
的横坐标为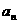
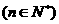
(1)求数列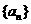 的通项公式
的通项公式
(2)设数列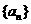 的前
的前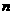 项和为
项和为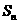 ,求证:
,求证:
(3)求证: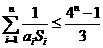
22、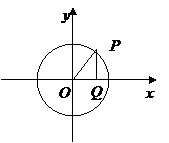 已知点
已知点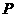 是圆
是圆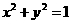 上的一个动点,过点
上的一个动点,过点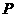 作
作 轴于点
轴于点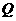 ,设
,设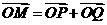
(1)求点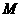 的轨迹方程
的轨迹方程
(2)求向量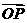 和
和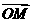 夹角的最大值,并求此时
夹角的最大值,并求此时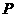 点的坐标
点的坐标
(3)判断函数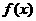 的单调性,并用单调性的定义证明你的结论。
的单调性,并用单调性的定义证明你的结论。
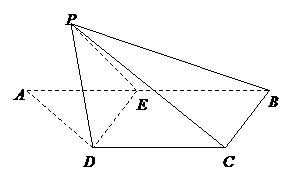
21、如图,梯形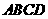 中,
中,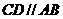 ,
,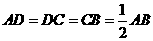 ,
,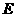 是
是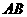 的中点,将
的中点,将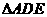 沿
沿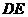 折起,使点
折起,使点 折到点
折到点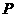 的位置,且二面角
的位置,且二面角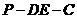 的大小为
的大小为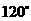
 (1)求证:
(1)求证: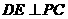
(2)求直线 与平面
与平面 所成角的大小
所成角的大小
(3)求点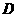 到平面
到平面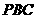 的距离
的距离
20、已知函数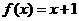 ,设
,设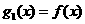 ,
,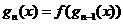
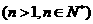
(1)求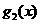 ,
,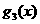 的表达式,并猜想
的表达式,并猜想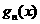
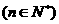 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于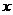 的函数
的函数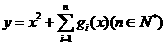 在区间
在区间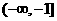 上的最小值为6,求
上的最小值为6,求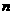 的值。
的值。
(符号“ ”表示求和,例如:
”表示求和,例如: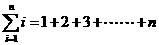 。)
。)
19、已知函数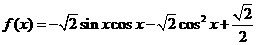
(1)求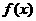 的单调增区间
的单调增区间
(2)在直角坐标系中画出函数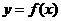 在区间
在区间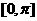 上的图象。
上的图象。
18、若函数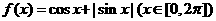 的图象与直线
的图象与直线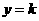 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则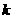 的取值范围是__________
的取值范围是__________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com