2. 设命题甲:△ABC的一个内角为60^o，命题乙:△ABC的三个内角的度数成等差数列.那么(　 )(88年(11)3分)

(A)甲是乙的充分不必要条件　　　　　　 (B)甲是乙的必要不充分条件 (C)甲是乙的充要条件　　　　　　　　　 (D)甲不是乙的充分条件也不是乙的必要条件

1. 给出20个数:87，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，88.它们的和是(　 )(86年(5)3分)

(A)1789　　　　　 (B)1799　　　　　 (C)1879　　　　　　 (D)1899

22．(1)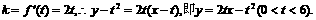………2分

　 (2)令y=0得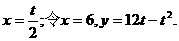

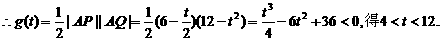　又0<t<6,

∴4<t<6，g(t)在(m, n)上单调递减，故(m, n)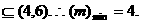…………8分

(3)当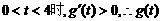在(0，4)上单调递增，

∴P的横坐标的取值范围为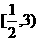.……………………………………………………14分

21．(1)设动点N的坐标为(x,y)，则　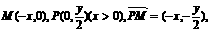 …………………2分

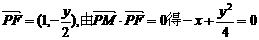，因此，动点的轨迹方程为 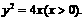……4分

(2)设l与抛物线交于点A(x₁,y₁),B(x₂,y₂)，当l与x轴垂直时，

则由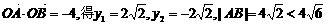， 不合题意，

故与l与x轴不垂直，可设直线l的方程为y=kx+b(k≠0),则由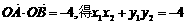…6分

由点A，B在抛物线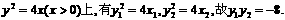

又y²=4x, y=kx+b得ky²－4y+4b=0,……………………8分

所以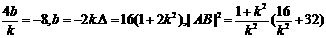……10分

因为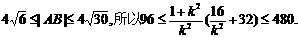解得直线l的斜率的取值范围是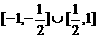.………………………………………………………………12分

20．(1)①门票收入为120万元的概率为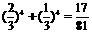………………………15分

　 (2)门票收入不低于180万元的概率

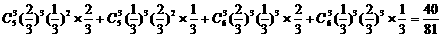…12分

18．证明：(1)S₃=3a₁, S₉=9a₁, S₆=6a₁, 而a₁≠0，所以S₃，S₉，S₆不可能成等差数列……2分

所以q≠1，则由公式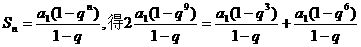……4分

即2q⁶=1+q³　 ∴2q⁶a₁q=a₁q+q³a₁q , ∴2a₈=a₂+a₅　 所以a₂, a₈, a₅成等差数列…………6分

(2)由2q⁶=1+q³=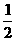－……………………………………………………………………8分

要以a₂, a₈, a₅为前三项的等差数列的第四项是数列{a_n}中的第k项，

必有a_k－a­₅=a₈－a­₂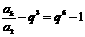,所以 所以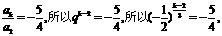

由k是整数，所以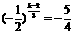不可能成立，所以a₂, a₈, a₅ 为前三项的等差数列的第四项不可能也是数列{a_n}中的一项.………………………………………………………12分

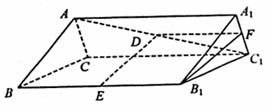　 19．(1)取A₁C₁中点F，连结B₁F，DF，

∵D，E分别为AC₁和BB₁的中点，

∴DF//AA₁，DF=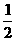AA₁

　 B₁E//AA₁，B₁E=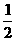AA₁，∴DF//B₁E，DF=B₁E，∴DEB₁F为平行四边形，……………………2分

∴DE//B₁F，又∵B₁F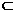平面A₁B₁C₁，DE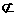平面A₁B₁C₁，∴DE//平面A₁B₁C₁.……4分

(2)连结A₁D，A₁E，在正三棱柱ABC-A₁B₁C₁中，

∵平面A₁B₁C₁⊥平面ACC₁A₁，A₁C₁是平面A₁B₁C₁与平面ACC₁A₁的交线，

又∵B₁F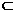平面A₁B₁C₁，且B₁F⊥A₁C₁，∴B₁F⊥平面ACC₁A₁，又DE//B₁F，∴DE⊥平面ACC₁A₁，

∴∠FDA₁为二面角A₁-DE-B₁的平面角，…………8分　 并且∠FDA₁=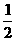∠A₁DC₁，

设正三棱柱的棱长为1，∵∠AA₁C₁=90°，D是AC₁中点，

∴DC­_­1=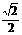，A₁D=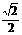_，∠A₁DC₁=90°∴∠FDA₁=45°，即二面角A₁-DE-B₁为45°.………12分

17．(1)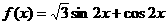…………………………………………4分

　 (2)在每个闭区间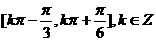…………………………8分

　 (3)将函数y=2sinx的图象向左平移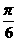个单位，再将得到的函数图象上的所有的点的纵坐标不变，横坐标缩短为原来的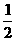………………………………………………12分

1．D　 2．A　 3．D　　 4．D　 5．C　 6．D　 7．C　 8．C　 9．B　 10．C　 11．B　 12．B

22．(本小题满分14分)

如图所示，曲线段OMB是函数f(x)=x²(0<x<6)的图象，BA⊥x轴于A，曲线段OMB上一点M(t, f(t)处的切线PQ交x轴于P，交线段AB于Q.

(1)试用t表示切线PQ的方程；

(2)设△QAP的面积为g(t)，若函数g(t)在(m , n)上单调递减，试求出m的最小值；

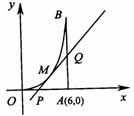　 (3)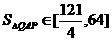，试求出点P横坐标的取值范围.

数 学 试 卷(理科农医类)答案

21．(本小题满分12分)

已知定点F(1，0)，动点P在y轴上运动，过点P作PM交x轴于点M，并延长MP到点N，且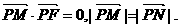

(1)动点N的轨迹方程；

(2)线l与动点N的轨迹交于A，B两点，若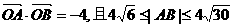，求直线l的斜率k的取值范围.