
题目列表(包括答案和解析)
16. (本小题满分14分)
由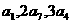 成等差数列, 得
成等差数列, 得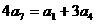 ,即
,即 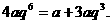 --- 2分
--- 2分
变形得 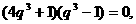 所以
所以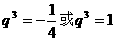 (舍去). --- 4分
(舍去). --- 4分
(1) 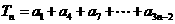
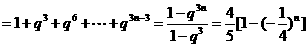 ;
;
--- 4分
(2) 由
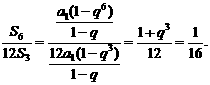
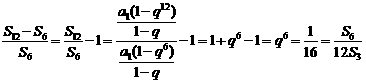 ,
,
所以12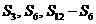 成等比数列.
--- 4分
成等比数列.
--- 4分
15. (本小题满分14分)
(1) 由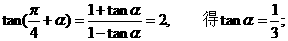 --- 5分
--- 5分
(2) 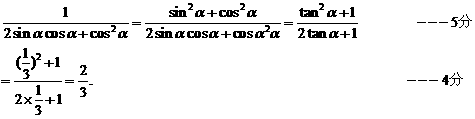
13. 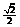 .
14. (24.2,0,0 )
.
14. (24.2,0,0 )
11. 如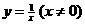 或
或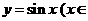 R)等. 12.
R)等. 12. 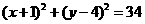 .
.
20. (本小题满分14分)
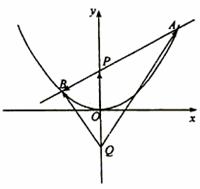 (第20题) |
如图,过抛物线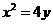 的对称轴上任一点
的对称轴上任一点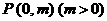 作直线与抛物线交于
作直线与抛物线交于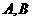 两点,点
两点,点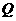 是点
是点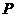 关于原点的对称点.
关于原点的对称点.
(1) 设点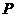 分有向线段
分有向线段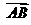 所成的比为
所成的比为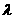 ,证明:
,证明:
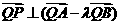 ;
;
(2) 设直线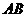 的方程是
的方程是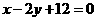 ,过
,过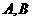 两点的圆
两点的圆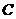 与抛物线在点
与抛物线在点 处有共同的切线,求圆
处有共同的切线,求圆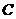 的方程.
的方程.
2006年杭州市第二次高考科目教学质量检测
数学参考评分标准(文科)
19. (本小题满分14分)
已知奇函数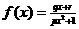 有最大值
有最大值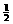 , 且
, 且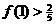 , 其中实数
, 其中实数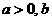 是正整数.
是正整数.
(1)
求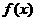 的解析式;
的解析式;
(2)
令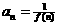 , 证明
, 证明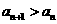 (
(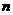 是正整数).
是正整数).
18. (本小题满分14分)
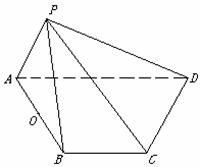 (第18题) |
如图, 在四棱锥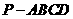 中,顶点
中,顶点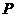 在底面
在底面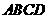 上的射影恰好落在
上的射影恰好落在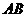 的中点
的中点 上,又∠
上,又∠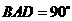 ,
,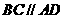 ,且
,且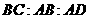
=1:2:2.
(1) 求证: 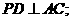
(2) 若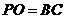 , 求直线
, 求直线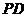 与
与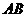 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面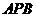 与平面
与平面 所成的角为
所成的角为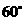 , 求
, 求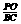 的值.
的值.
17.(本小题满分14分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
(1) 三人各向目标射击一次,求至少有一人命中目标的概率;
(2) 三人各向目标射击一次,求恰有两人命中目标的概率;
(3)若甲单独向目标射击三次,求他恰好命中两次的概率.
16. (本小题满分14分)
已知数列{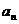 }是首项为
}是首项为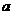 等于1且公比
等于1且公比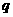 不等于1的等比数列,
不等于1的等比数列,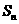 是其前
是其前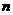 项的和,
项的和,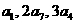 成等差数列.
成等差数列.
(1) 求和 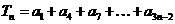 ;
;
(2) 证明 12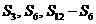 成等比数列.
成等比数列.
15. (本小题满分14分)
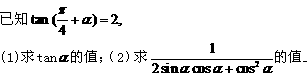
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com