
题目列表(包括答案和解析)
22. (本题满分13分)
(理科)已知椭圆的两个焦点分别为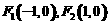 ,过
,过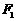 的直线
的直线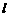 交椭圆于点M、N,
交椭圆于点M、N,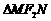 的周长为8.过
的周长为8.过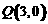 的直线m交椭圆于不同的两点A、B.
的直线m交椭圆于不同的两点A、B.
|
|
(2)OA·OB = 0能否成立(O为原点)?若能成立,求出此时直线m的方程;若不能
|
|
|
|
|
 (3)若在x轴上存在一点C,使AB·(CA+ AB)= 0成立,求|OC|的取值范围.
(3)若在x轴上存在一点C,使AB·(CA+ AB)= 0成立,求|OC|的取值范围.
[解析]
(1)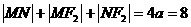 --------2分
--------2分 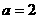 ,
,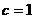 ,
,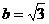 -
-
所以椭圆的方程为: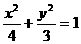 ---------3分
---------3分
(2)若直线 :
: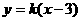 使
使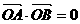 成立,设
成立,设 ,
,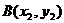
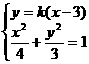 消去
消去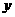 得:
得: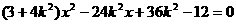
由 ,得
,得 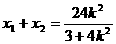 ,
,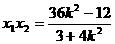
∵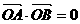 ∴
∴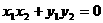
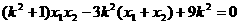 解得
解得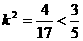
故存在直线 :
: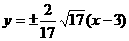 满足条件。-------8分
满足条件。-------8分
-(3)由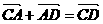 故
故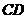 垂直
垂直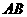
直线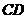 的方程为:
的方程为: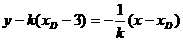
令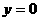 ,得
,得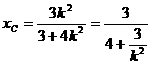
因为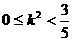 ,所以
,所以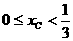 故
故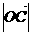 的取值范围为
的取值范围为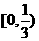 -----13分
-----13分
[评析] 本题综合考查了椭圆的定义、标准方程、直线与椭圆、向量等知识的灵活运用,运用韦达定理设而不求是处理直线与圆锥曲线位置关系,是解析几何中减少运算量一种重要手段。
(文科)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足
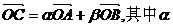 、
、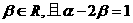
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线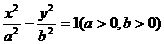 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: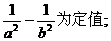
(3)在(2)的条件下,若双曲线的离心率不大于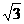 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
(1)解:设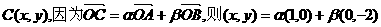
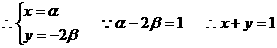
即点C的轨迹方程为x+y=1……(4分)
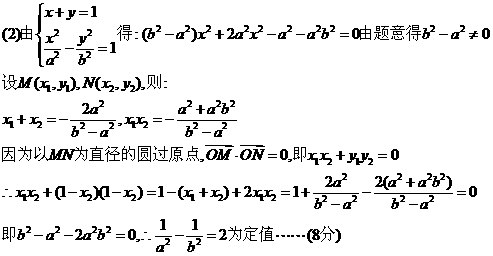
(3)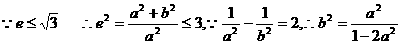
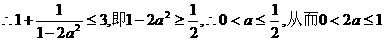
∴双曲线实轴长的取值范围是(0,1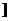 ………………(13分)
………………(13分)
[评析] 本题综合考查了向量与点的轨迹、直线与圆锥曲线的位置关系的灵活运用、椭圆的几何性质等,要注意综合分析后,采用适当的方法减少运算量.
[命题报告]
命题前对近几年来高考的热点、难点和重点进行了全面的研究,命题时依据最新的《考试大纲》的各项要求,.融入了新课程新大纲的理念,在注重对基础知识的全面考查的同时,注重对考生创造性地解决问题能力的考查。
21.(本题满分13分)
(理科)已知 ,数列{an}满足:
,数列{an}满足: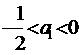 ,
,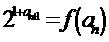 ,
,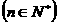 .
.
(1)
求证: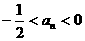
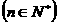 .
.
(2)
判断an与an+1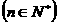 的大小,并说明理由。
的大小,并说明理由。
[解析]
|
|

由①,②可知,
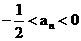 对于任意
对于任意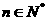 都成立.
都成立.
|
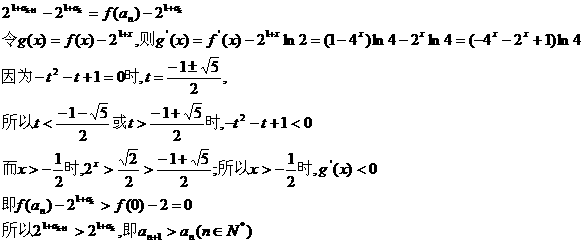 [评析] 本题在函数、数列、不等式等知识交汇处命题,综合考查考生分析解决问题的能力。在数学归纳法中运用求导是本题的新亮点,探询传统知识和新增知识的整合在本题得到较完美的体现。
[评析] 本题在函数、数列、不等式等知识交汇处命题,综合考查考生分析解决问题的能力。在数学归纳法中运用求导是本题的新亮点,探询传统知识和新增知识的整合在本题得到较完美的体现。
(文科)定义:若数列 对任意
对任意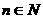 ,满足
,满足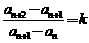 (k为常数),则称数列
(k为常数),则称数列 为等差比数列.
为等差比数列.
(1)若数列 的前n 项和
的前n 项和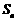 满足
满足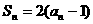 ,求
,求 的通项公式,并判断数列
的通项公式,并判断数列
是否为等差比数列;
(2)若数列 为等差数列,试判断
为等差数列,试判断 是否一定为等差比数列,并说明理由;
是否一定为等差比数列,并说明理由;
(3)试写出一个等差比数列的通项公式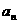 ,使此数列既不是等差数列,也不是等比数列.
,使此数列既不是等差数列,也不是等比数列.
[解析]
(1)当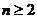 时,
时,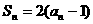 ①,
①,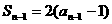 ②-
②-
①-②得: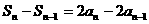 所以
所以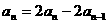
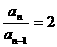
又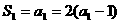 ,所以
,所以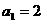 ,所以
,所以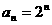 (
(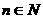 )
)
∵任给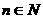 ,
,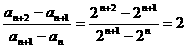 ∴数列
∴数列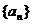 为等差比数列…..5分
为等差比数列…..5分
(2)令等差数列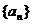 的公差为
的公差为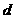 ,则
,则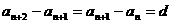
当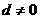 时,
时,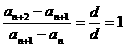 (1为常数),所以数列
(1为常数),所以数列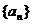 是等差比数列-
是等差比数列-
当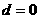 ,即数列
,即数列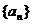 是常数数列时,不是等差比数列。。。。。。。。10分
是常数数列时,不是等差比数列。。。。。。。。10分
(3)通项如 形式的数列,如
形式的数列,如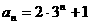 ,不是等差数列,也不是等比数列,但
,不是等差数列,也不是等比数列,但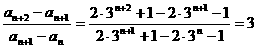 为常数。
为常数。
数列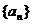 是等差比数列--------------13分(只要写出一个通项即可)
是等差比数列--------------13分(只要写出一个通项即可)
[评析] 本题设计新颖,既考查了数列中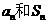 的关系问题等数列的基础知识,又考查了考生理解和学习新知识的能力。
的关系问题等数列的基础知识,又考查了考生理解和学习新知识的能力。
19. (本题满分12分)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
[解析]
解法一:(Ⅰ)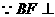 平面ACE.
平面ACE. 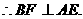
∵二面角D-AB-E为直二面角,且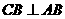 ,
, 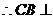 平面ABE.
平面ABE.
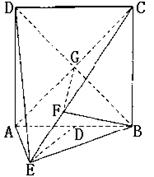
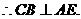
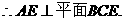
(Ⅱ)连结BD交AC于C,连结FG,
∵正方形ABCD边长为2,∴BG⊥AC,BG=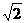 ,
,
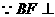 平面ACE,
平面ACE,
由三垂线定理的逆定理得FG⊥AC.
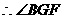 是二面角B-AC-E的平面角.
是二面角B-AC-E的平面角.
由(Ⅰ)AE⊥平面BCE, 又 ,
,
∴在等腰直角三角形AEB中,BE=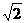 .
.
又 直角
直角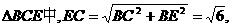
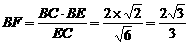 ,
,
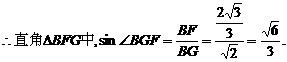
∴二面角B-AC-E等于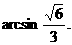
(Ⅲ)过点E作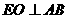 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,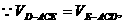
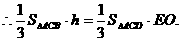
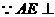 平面BCE,
平面BCE,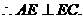
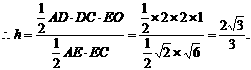
∴点D到平面ACE的距离为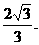
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直
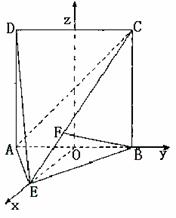 线为x轴,AB所在直线为y轴,过O点平行
线为x轴,AB所在直线为y轴,过O点平行
于AD的直线为z轴,建立空间直角坐标系
O-xyz,如图.
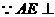 面BCE,BE
面BCE,BE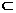 面BCE,
面BCE, 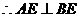 ,
,
在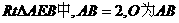 的中点,
的中点,
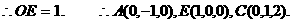
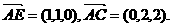 设平面AEC的一个法向量为
设平面AEC的一个法向量为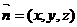 ,
,
则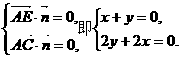
解得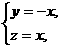
令 得
得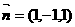 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为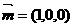 ,
,

∴二面角B-AC-E的大小为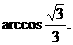
(III)∵AD//z轴,AD=2,∴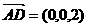 ,
,
∴点D到平面ACE的距离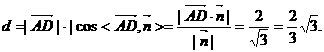
[评析]新课程引入空间向量后,为几何问题代数法解决提供了更家易于掌握的方法,拓宽了我们的解题思路,特别是立体几何中的动点问题,运用空间向量更能使问题得到简捷解决。同学们应该把立体几何解答题列为必得分题。
18. (本题满分12分)
设函数
(1)求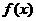 的单调区间和极值;
的单调区间和极值;
(2)讨论方程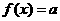 的实根的个数.
的实根的个数.
[解析](1)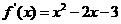 ;由
;由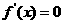 ,得x=-1或x=3.............2分
,得x=-1或x=3.............2分
列表如下:
|
x |
(-∞,-1) |
-1 |
(-1, 3) |
3 |
(3,+ ∞) |
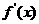 |
- |
0 |
+ |
0 |
- |
|
f(x) |
 |
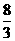 |
 |
-8 |
 |
∴函数f(x)的极大值为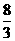 ,极小值为-8
,极小值为-8
函数f(x)单调递增区间是(-∞,-1)和(3,+ ∞),递减区间是(-1, 3)……(6分)
(2)令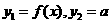 ,根据(1)的分析,可在同一坐标系内作出它们的大致图象,其中
,根据(1)的分析,可在同一坐标系内作出它们的大致图象,其中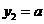 是一条与x轴平行的可移动的平行直线.
是一条与x轴平行的可移动的平行直线.
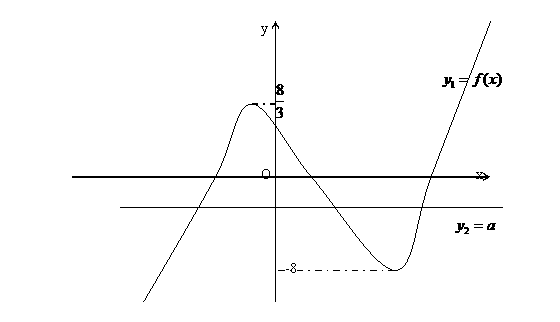

…………………………………………………………………………….9分
∴①当a=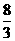 或a=-8时,原方程有且仅有两个不相等的实数根;……10分
或a=-8时,原方程有且仅有两个不相等的实数根;……10分
②当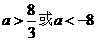 时,原方程有且仅有一个实数根;……………………11分
时,原方程有且仅有一个实数根;……………………11分
③当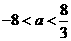 时,原方程有三个实数根……………………………………12分
时,原方程有三个实数根……………………………………12分
[评析]本题考查了导数的运用及三次方程实数根的情况,为利用导数知识来分析三次方程的实根个数提供了新的研究视角。第一问属于基础知识,第二问,借助数形结合的方法,把方程根的个数问题转化为图象交点个数问题,并利用导数知识,分析三次函数的性质,从而作出三次函数的大致图象,为数形结合解决问题提供了保证。
17. (本题满分12分)
已知向量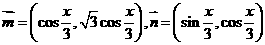 ,
,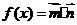
(1) 求函数f (x)的单调递增区间并求其图象对称中心的横坐标;
(2) 如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f (x)的值域.
[解析]
(1) 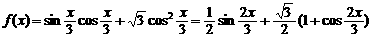 ………………..2分
………………..2分
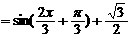 ………………………………………………4分
由
………………………………………………4分
由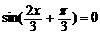 得:
得: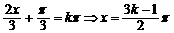 (k∈Z)
∴对称中心的横坐标为
(k∈Z)
∴对称中心的横坐标为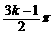 (k∈Z).………………………………………………5分
(k∈Z).………………………………………………5分
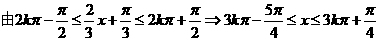
∴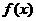 的单调递增区间是
的单调递增区间是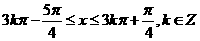 …………………….. 6分
(2)由已知得
…………………….. 6分
(2)由已知得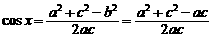 ≥
≥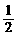 …………………………………8分
又x是△ABC的内角,∴x的取值范围是
…………………………………8分
又x是△ABC的内角,∴x的取值范围是 …………………………………….10分
这时,
…………………………………….10分
这时,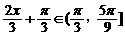 ,∴
,∴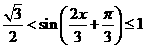 故函数f (x)的值域是
故函数f (x)的值域是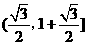 .………………………………………………….12分
.………………………………………………….12分
[评析]本题是立足于向量与三角知识及不等式等知识交汇处设计的一道好题。它以向量的数量积为媒介,考查运用三角变换与化一公式及余弦定理、均值不等式等求三角函数的性质与最值等知识。求范围问题中,常运用均值不等式,进行放缩转化,是高考中常用的解题技巧,要注意认真体会,并加以归纳总结。
16. 一个三棱锥三条侧棱两两垂直,其长分别为3,4,5,则它的外接球的表面积为50π
[解析]以三条两两垂直的侧棱为棱,将三棱锥补成长方体,则长方体的对角线就是外接球的直径即(2R)2=32+42+52=50,故S球=4πR2=50π
[评析]割补法是立体几何试题中求体积的常用方法.
三:解答题(本大题有6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)
15. 配置A、B两种药剂都需要甲、乙两种原料,用料要求如右表所示(单位:克),如果药剂A、B至少各配一剂,且药剂A、B每剂售价分别为2元,3元,现在有原料甲20克,原料乙25克,那么可以获得的最大销售额为17元.
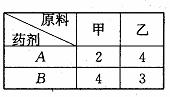
[解析]设药剂A,B分别配制x,y剂,目标函数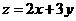 ,由题意可得
,由题意可得
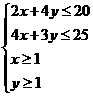
作出可行域,平行移动直线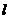 :
: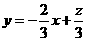 ,当直线
,当直线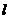 点(4,3)时符合题意.
点(4,3)时符合题意.
[评析]解答线性规划应用题,关键是根据线性约束条件建立可行域,然后运用数形结合知识加以解决.移动直线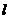 确定最优解是难点,可以把各边界点均解出来,把坐标逐一代入后确定,在运算量不太大时可运用此方法;也可转化为与直线
确定最优解是难点,可以把各边界点均解出来,把坐标逐一代入后确定,在运算量不太大时可运用此方法;也可转化为与直线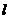 纵截距问题来解决,但是在画直线
纵截距问题来解决,但是在画直线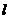 时要注意其斜率与边界直线斜率的关系,确定
时要注意其斜率与边界直线斜率的关系,确定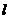 过边界点的倾斜程度,否则会导致错。
过边界点的倾斜程度,否则会导致错。
14. (理科)已知n元集合M={1,2,…,n},设M所有的3元子集的元素之和为Sn,
则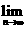 =
=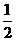
[解析] 集合M共有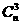 个三元子集,其中含1的三元子集有
个三元子集,其中含1的三元子集有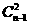 个,
个,
同理,含2,3,…,n的三元子集也各有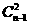 个,
个,
∴Sn=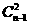 (1+2+…+n)=,
(1+2+…+n)=,
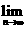 =
=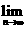 =
=
[评析]本题考查组合知识及数列极限的求法,属于中档题.
(文科)口袋中有红球2个,黑球3个,白球5个,它们只有颜色不同.从中摸出四个,摸出的球中同色的两个为一组,若红色一组得5分,黑色一组得3分,白色一组得1分,则得分总数取得最大值的概率为________________ [解析]要使得总分数取得最大,只有两个红球与两个黑球的取法, 其概率为P=.
[评析]概率型小应用题,贴近生活,是新高考的命题热点之一,解答本题的关键将“要使得总分数取得最大”转化为如何取球问题。
13.(理科)若数列{an}满足an+1=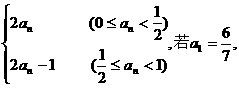 则a20的值是
则a20的值是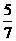
[解析]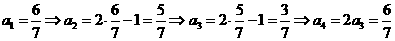 。
。
∴数列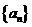 是周期为3的数列,∴
是周期为3的数列,∴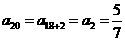 .
.
[评析]数列是特殊的函数,某些数列和函数一样具有周期性.分段函数求值时,一定根据定义域的约束条件,要对号入座。
(文科)设函数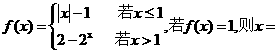 -2
-2
[解析] 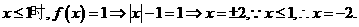
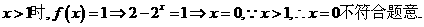
[评析]分段函数求值时,一定根据定义域的约束条件,要对号入座。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com