
题目列表(包括答案和解析)
19、(文)已知等比数列{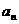 }的公比为q,前n项和为Sn,是否存在常数c,使数列{
}的公比为q,前n项和为Sn,是否存在常数c,使数列{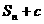 }也成等比数列?若存在,求出c的值;若不存在,说明理由.
}也成等比数列?若存在,求出c的值;若不存在,说明理由.
解:(1)当q=1时,不存在常数c,使数列{Sn+c}成等比数列;
(2)当q≠1时,存在常数c=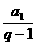 ,使数列{Sn+c}成等比数列.
,使数列{Sn+c}成等比数列.
(理)、已知数列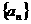 的前n项和为
的前n项和为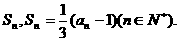 (Ⅰ)求
(Ⅰ)求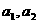 ;(Ⅱ)求证数列
;(Ⅱ)求证数列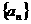 是等比数列
是等比数列
解: (Ⅰ)由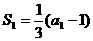 ,得
,得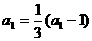 ,∴
,∴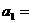
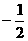 ,又
,又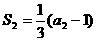 ,即
,即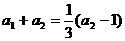 ,得
,得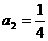 .(Ⅱ)当n>1时,
.(Ⅱ)当n>1时,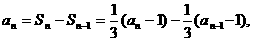 得
得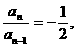 所以
所以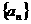 是首项
是首项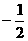 ,公比为
,公比为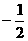 的等比数列
的等比数列
18、 (文)设f(x)=lg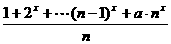 ,a
,a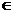 R, n
R, n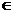 N且n
N且n 2.若f(x)当x
2.若f(x)当x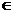 (-
(- ,1)有意义,求a的取值范围.
,1)有意义,求a的取值范围.
解: f(x)当x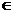 (-
(- ,1)有意义,当且仅当1+2
,1)有意义,当且仅当1+2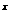 +…+(n-1)
+…+(n-1)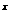 +an
+an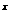 >0 对x
>0 对x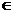 (-
(- ,1)恒成立.即函数
,1)恒成立.即函数
g(x)=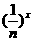 +
+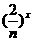 +…+
+…+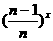 +a>0
+a>0
对于任意的x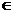 (-
(- ,1)恒成立.因为g(x)在(-
,1)恒成立.因为g(x)在(- ,1)上是减函数,
,1)上是减函数,
最小值为g(1)=
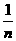 +
+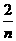 +…+
+…+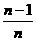 +a=
+a=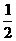 (n-1)+a,
(n-1)+a,
所以g(x)
>0对x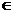 (-
(- ,1)恒成立的充要条件是
,1)恒成立的充要条件是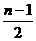 +a>0,即a>
+a>0,即a>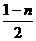 .
.
故所求实数a的范围为(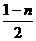 ,+
,+ )
)
17、设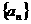 是一个公差为
是一个公差为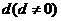 的等差数列,它的前10项和
的等差数列,它的前10项和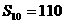 且
且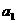 ,
,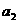 ,
,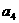 成等比数列。(1)证明
成等比数列。(1)证明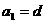 ;(2)求公差
;(2)求公差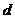 的值和数列
的值和数列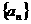 的通项公式
的通项公式
证明:因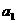 ,
,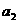 ,
,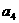 成等比数列,故
成等比数列,故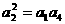 ,而
,而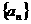 是等差数列,有
是等差数列,有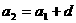 ,
,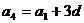
于是 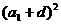
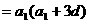 ,即
,即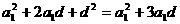 ,
,
化简得 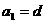

(2)解:由条件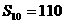 和
和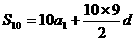 ,得到
,得到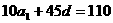 ,由(1),
,由(1),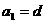 ,代入上式得
,代入上式得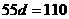 ,故
,故 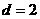 ,
,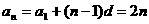 ,
,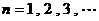

16.给出如下命题:
(1)如果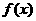 为奇函数,则其图象必过(0,0)点;
为奇函数,则其图象必过(0,0)点;
(2)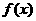 与
与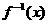 的图象若相交,则交点必在直线
的图象若相交,则交点必在直线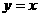 上;
上;
(3)若对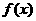 定义域内任意实数
定义域内任意实数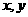 恒有
恒有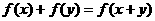 ,则
,则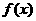 必为奇函数;
必为奇函数;
(4)函数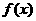 =
=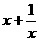 的极小值为2,极大值为-2.
的极小值为2,极大值为-2.
其中真命题的序号为 .(1)(2)(3)
15..已知数列{an}的前n项的和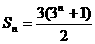 ,则数列{an}的通项
,则数列{an}的通项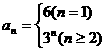
14、定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列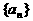 是等和数列,且
是等和数列,且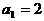 ,公和为5,那么
,公和为5,那么
(文)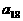 的值为___。
的值为___。
(理)这个数列的前18,19项和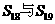 的值为了
的值为了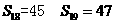
13.已知二次函数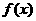 满足
满足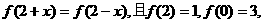 如果
如果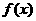 在区间
在区间
[0,m]上最小值为1,最大值为3,则m的取值范围是 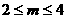
22.(本题满分14分)圆锥曲线C的一个焦点为F(2,0),相应的准线是直线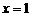 ,以过焦点F并与
,以过焦点F并与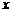 轴垂直的弦为直径的圆截准线
轴垂直的弦为直径的圆截准线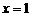 所得弦长为2。
所得弦长为2。
(Ⅰ)求圆锥曲线C的方程;
(Ⅱ)当过焦点F的直线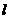 的倾斜角
的倾斜角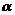 在何范围内取值时,圆锥曲线C上有且只有两个不同的点关于直线
在何范围内取值时,圆锥曲线C上有且只有两个不同的点关于直线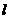 对称?
对称?
21.(本小题满分12 分)某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,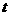 小时内供水总量为
小时内供水总量为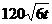 吨,(
吨,(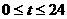 )
)
(Ⅰ)从供水开始到第几小时,蓄水池中的存水量最少?最少水量是多少吨?
(Ⅱ)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。
20.(本题12分)已知函数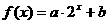 的图像经过点
的图像经过点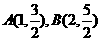
(1)求函数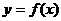 的反函数;
的反函数;
(2)设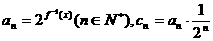 ,求数列
,求数列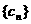 的前n项和Sn.
的前n项和Sn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com