22．(本题14分)已知双曲线C的中心在原点，抛物线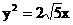的焦点是双曲线C的一

个焦点，且双曲线过点(1, )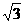

(1)求双曲线的方程;

(2)设直线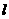: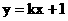与双曲线C交于A、B两点, 试问:

① 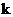为何值时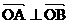

② 是否存在实数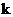, 使A、B两点关于直线对称(为常数), 若存在, 求出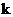

21. (本题12分)运货卡车以每小时x千米的速度匀速行驶130千米, 按交通法规限制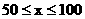(单位: 千米/小时). 假设汽油的价格是每升2元, 而汽车每小时耗油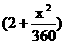升, 司机的工资是每小时14元.

(1) 求这次行车总费用y关于x的表达式；

(2) 当x为何值时, 这次行车的总费用最低, 并求出最低费用的值.

(精确到小数点后两位,)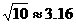

20． (本题12分)在棱长为4的正方体ABCD-A₁B₁C₁D₁中, O是正方形A₁B₁C₁D₁的中心, 点

P在棱CC₁上, 且CC₁＝4CP.

(1) 求直线AP与平面BCC₁B₁所成的角的大小 (结果用反三角函数值表示);

(2) 设O点在平面D₁AP上的射影是H, 求证: D₁H⊥AP；

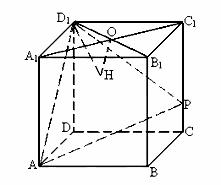(3) 求点P到平面ABD₁的距离.

19．(本题12分) 等差数列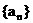是递增数列，前n项和为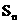, 且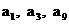成等比数列,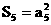 　

(1)求数列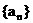的通项公式;

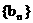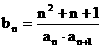(2)若数列满足求数列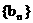的前99项的和.

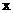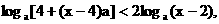18． (本题12分) 解关于的不等式 其中.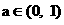

17．(本题12分)已知函数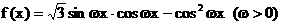

最小正周期.

(1) 求实数的值;

(2) 若x是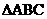的最小内角, 求函数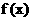的值域.

16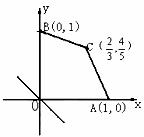．给出平面区域如图所示, 目标函数为: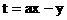

若当且仅当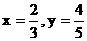时, 目标函数t取最小值,

则实数a的取值范围是　　　　　　　　　　 .

15．已知a、b为不垂直的异面直线, 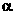是一个平面, 则a、b在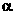上的射影有可能是

①两条平行直线 ②两条互相垂直的直线 ③同一条直线 ④一条直线及其外一点称

在上面结论中, 正确结论的编号是　 　　　　　　　　.(写出所有正确结论的编号)

14．已知椭圆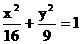的左、右焦点分别为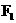、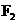, 点P在椭圆上. 若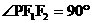是

一个直角三角形的三个顶点, 则点P到x轴的距离为　　　　　　　　 .

13．设a、b、c分别是△ABC的∠A、∠B、∠C的对边边长, 则直线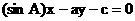

与直线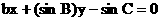的夹角大小是　　　　　　　　　 .