
题目列表(包括答案和解析)
7.求和: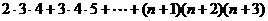 =( )。
=( )。
6.求和: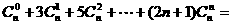 ( )。
( )。
5.已知数列 是首项为3,公差为2的等差数列,则
是首项为3,公差为2的等差数列,则
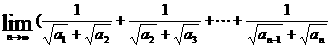 )=( )。
)=( )。
4.求和: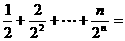 (
)。
(
)。
a)
已知数列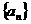 的前
的前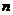 项和
项和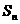
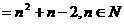 ,则正确的是
,则正确的是
(A)数列 是等差数列
(B)数列
是等差数列
(B)数列 是等比数列
是等比数列
(C) 数列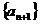 是等差数列 (D)数列
是等差数列 (D)数列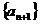 是等比数列
是等比数列
b)
已知数列 的前
的前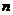 项和
项和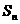 =
=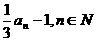 ,那么
,那么
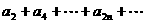 的值是
的值是
(A)-3 (B)-1 (C)3 (D)1
c)
数列 的前
的前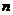 项和
项和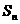 为
为
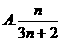
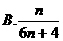
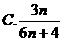
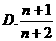
5.(2000广东)设数列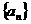 为等比数列,
为等比数列,
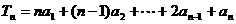 ;已知
;已知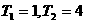 ,
,
(1) 数列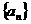 的首项与公比。
的首项与公比。
(2) 求数列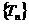 的通项公式。
的通项公式。
解析:(1)易知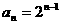 。
。
(3) 采用错位相减法。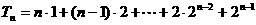
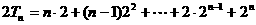
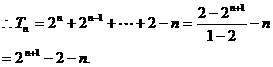
4.(99全国春季高考)已知函数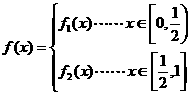
其中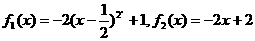
① 画出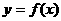 的图象。
的图象。
② 设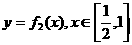 的反函数为
的反函数为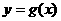 ,
,
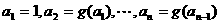 ;求数列
;求数列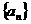 的通项公式。
的通项公式。
解析:①略。
②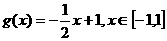
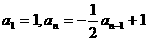
由待定系数法得: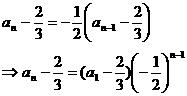
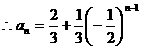
3.(89全国)是否存在常数a、b、c,使得等式
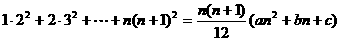 ,对一切自然数n都成立?
,对一切自然数n都成立?
并证明你的结论。
解析:此题的思路有两种:一种是考虑归纳-猜测-证明法。一种是直接求和法。
下面给出一种直接求和法:
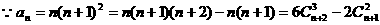
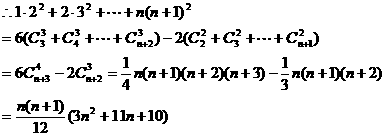
所以,存在常数a、b、c,使得等式
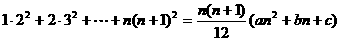 ,对一切
,对一切
自然数n都成立?
2.(94全国)设数列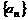 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为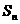 ,并且对于所有的自然数n,
,并且对于所有的自然数n,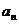 与2的等差中项等于
与2的等差中项等于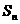 与2的等比中项。
与2的等比中项。
(1) 写出数列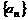 的前三项。
的前三项。
(2) 求数列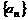 的通项公式。
的通项公式。
(3) 令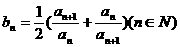 ,求
,求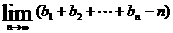 。
。
解析:(1)由题意:
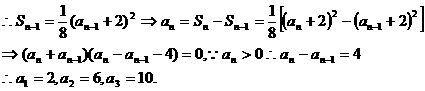
(2)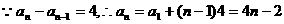 。
。
(3)
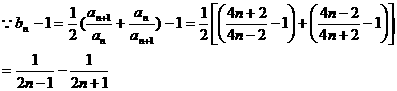
故
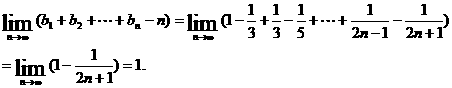
点评:(1)已知数列 的前
的前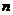 项和
项和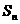 与通项
与通项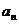 的关系时,最好是先转化为递推公式,然后在由递推公式求通项公式。当然,此题也可直接求出前三项,然后猜测通项公式,并用数学归纳法证明。
的关系时,最好是先转化为递推公式,然后在由递推公式求通项公式。当然,此题也可直接求出前三项,然后猜测通项公式,并用数学归纳法证明。
(2)本题的数列求和采用的是裂项求和法。
1. (93上海)设数列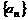 的前n项和
的前n项和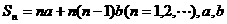 是常数,且
是常数,且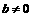
(1)
证明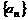 是等差数列。
是等差数列。
(2)
证明以(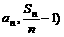 为坐标的点
为坐标的点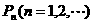 都落在同一条直线上,并写出此直线方程。
都落在同一条直线上,并写出此直线方程。
(3) 设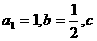 是以
是以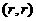 为圆心,r为半径的圆
为圆心,r为半径的圆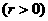 ,求使得点P1,P2,P3都落在圆C外时,r的取值范围。
,求使得点P1,P2,P3都落在圆C外时,r的取值范围。
解析:(1)
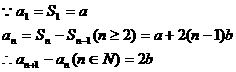
所以,数列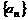 是等差数列。
是等差数列。
(2)略,(3)详解略,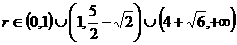 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com