16.解析: ①展开式的通项公式为T_r+1=(－1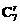)^r2^7－r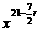(r=0,1,2),令21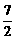－r=0得r=6,即常数项为T₇,∴①假.

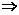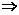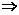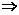
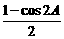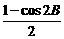
②在△ABC中,A＞Ba＞b2RsinA＞2RsinB＞0sin²A＞sin²B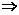＞cos2A＜cos2B,②真.

③由抛物线y=f(x)=x²－x+a的对称性知点(m,f(m))和点(1－m,f(1－m))关于直线x=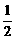对称,∴f(1－m)=f(m)＞0,③真.

④连结空间四边形ABCD的对角线AC·BD后,得棱锥A-BCD是棱长为a的正四面体,在侧面ABC内, 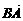与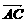的夹角为120°,∴2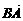·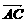=－a²,∴④假.

答案: ②③

14.解析: B队获胜的形式可以有三种:3∶2获胜,3∶1获胜,3∶0获胜.

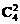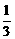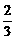①3∶2获胜,必须打满5局,且最后一局是B队胜,故3∶2获胜的概率为P=()²·()²·=.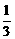

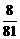②3∶1获胜,只需打4局,且最后一局是B队胜,故3∶1获胜的概率为P=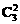(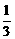)²··=.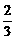

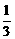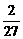③3∶0获胜,则必须第1~3局B均胜才行,故3∶0获胜的概率为P=(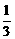)³=.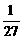

B队获胜的概率为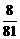++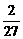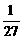=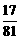.　 答案:

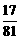
15解析: 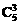++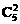+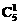1=26.　 答案: 26

13.解析: 由f(x)的解析式可知f(x)图象连续及f(x)的单调性可确定,在(－1,1)和(2,+∞)上均有f(x)＞0.

答案: (－1,1)∪(2,+∞)

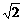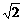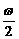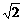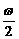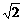12.解析: 由题意有A=,sin(－+φ)=0,sin(+φ)=,∴φ=,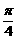

ω=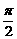,f(x)=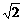sin(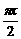+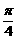),最小正周期T=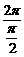=4,f(0)=1,f(1)=1,f(2)=－1,f(3)=－1. ∴原式=f(0)+f(1)=2.　　 答案: C

11.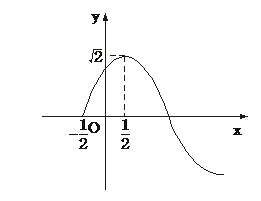解析: 一枚骰子先后掷两次,其基本事件(b,c)的总数是36,且是等可能的.方程有实根的充分必要条件是b²－4c≥0,即c≤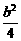,满足该条件的基本事件的个数为:

①b=1时有0个;②b=2时有1个;③b=3时有2个;④b=4时有4个;⑤b=5时有6个;⑥b=6时有6个,共19个.答案: C

10. 解析: 曲线是右半单位圆和下半单位圆的并集,右半单位圆方程是x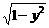－=0(x≥0);下半单位圆方程是y+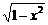=0(y≤0).　 答案: D

9. 解析: 设正方形ABCD的边为长1,则AC=2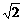c=,c=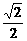,2a=|PA|+|PC|=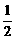+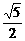, a=+

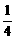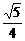,∴e=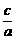=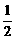(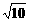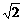－).答案: C

8.解析: 由已知可得f(x₁)+f(x₂)+…+f(x₂₀₀₅)=8,

又f(x₁²)+f(x₂²)+…+f(x₂₀₀₅²)

=2［f(x₁)+f(x₂)+…+f(x₂₀₀₅)］

=2×8=16.　 答案: C

7.解析: 依定义:f(x)=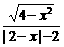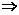|x|≤2且x≠0,∴f(x)=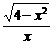－为奇函数. 答案: A

6.解析: 解法一:设A、B、C分别表示“甲被录取”“乙被录取”“丙被录取”三个命题.则判断①为非A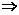B且C;判断②为非B或非C为真;判断③为非A或B为真.

①的逆否命题为非B或非C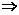A,结合②可知A为真,即甲被录取.由A真可知非A为假,结合③可知B为真,即乙被录取.

解法二:根据判断①.若甲未被录取,则乙与丙都被录取,这与②矛盾.故甲被录取.由于③正确,故“甲未被录取”与“乙被录取”中至少一个正确.由于“甲未被录取”不正确,故“乙被录取”正确.　 答案: D