20.(本小题满分14分)

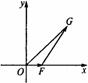　 以O为原点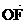，所在直线为x轴，建立如图所示的直角坐标系.设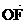·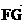=1，点F的坐标为(t，0)，t∈[3，+∞)，点G的坐标为(x₀，y₀).

　 (1)求x₀关于t的函数x₀=f(t)的表达式，判断函数f(t)的单调性，并证明你的判断；

　 (2)设△OFG的面积S=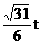，若以O为中心，F为焦点的椭圆经过点G，求当|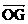|取得最小值时椭圆的方程；

　 (3)在(2)的条件下，若点P的坐标为(0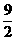，)，C、D是椭圆上的两点，且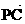=λ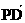(λ≠1)，求实数λ的取值范围.

19.(本小题满分14分)

　 (1)已知等比例{a_n}的公比为q，前n项和为S_n，是否存在常数C，使数列{S_n+C}也成比数列？若存在，求出C的值；若不存在，说明理由.

　 (2)设等比例数列{a_n}的前n项和为S_n.已知S₃，S₉，S₈成等差数列，S₁₆-S₆，S₁₀，xS₅成等比数列，求x的值.

18.(本小题满分14分)

　 设函数f(x)=-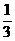x³+2ax²-3a²x+b，0＜a＜1.

　 (1)求函数f(x)的单调区间、极值；

　 (2)若当x∈[a+1，a+2]时，恒有|f＇(x)|≤a，试确定a的取值范围.

17.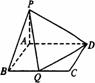(本小题满分14分)

　 如图所示，在矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD，PA=1.

　 (1)在BC边上是否存在点Q，使得PQ⊥QD，说明理由；

　 (2)若BC边上有且仅有一个点Q，使PQ⊥QD，求AD与平面PDQ所成角的正弦值；

　 (3)在(2)的条件下，能求出平面PQD与平面ABP所成的角的大小吗？

16.(本小题满分14分)

　 一个通讯小组有两套设备，只要其中有一套设备能正常工作，就能进行通讯.每套设备由3个部件组成，只要其中有一个部件出故障，这套设备就不能正常工作.如果在某一时间段内每个部件不出故障的概率为p，计算这一时间段内：

　 (1)恰有一套设备能正常工作的概率；

　 (2)能进行通讯的概率.

15.(本小题满分14分)

　 已知向量a=(cosα，sinα)，b=(cosβ，sinβ)，|a-b|=.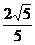

　 (1)求cos(α-β)的值；

　 (2)若0＜α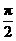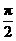＜，-＜β＜0，且sinβ=-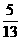，求sinα的值.

14.设函数f(x)=lg(x²+ax-a-1)，给出下列命题：①f(x)有最小值；②当a=0时，f(x)值域为R；③当a＞0时，f(x)在[2，+∞)上有反函数；④若f(x)在区间[2，+∞)上单调递增，则实数a的取值范围是a≥-4，其中正确命题的序号为______.

13.在(1-x)(1+x)¹⁰的展开式中，x³的系数为______.(用数字作答)

12.某中学有高一学生400人，高二学生300人，高三学生300人，现通过分层抽样取一个样本容量为n的样本，已知每个学生被抽到的概率为0.2，则n=______.

11.已知|a|=3，|b|=5，且a·b=12，则a在b的方向上的投影为______.