21．(本小题满分12分)设函数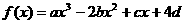 (a、b、c、d∈R)图象关于

原点对称，且x=1时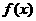，取极小值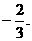

　 (1)求a、b、c、d的值；

　 (2)当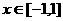时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明

你的结论；

　 (3)若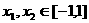时，求证：.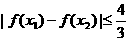

20．(本小题满分12分)已知向量.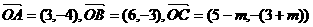

①若点A、B、C能构成三角形，求实数m应满足的条件；

②若△ABC为直角三角形，且∠A为直角，求实数m的值.

.

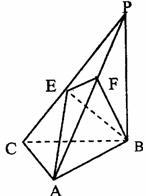
19．(本小题满分12分)已知三棱锥P-ABC中PB⊥底面ABC，，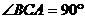

PB=BC=CA=a，E是PC的中点，点F在PA上，且3PF=FA.

　 (1)求证：平面PAC⊥PBC；

　 (2)求平面BEF与底面ABC所成角(用一个反三角函数值表示).

18．(本小题满分12分)设S_n是等差数列{a_n}的前n项和，已知a₃=6, S₉=36,

　 (1)写出数列{a_n}的通项公式；

　 (2)若b_n=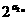证明数列{b_n}是等比数列，并求数列{b_n}的各项和.

17．(本小题满分12分)在人寿保险业中，要重视某一年龄的投保人的死亡率，经过随机抽

样统计，得到某城市一个投保人能活到75岁的概率为0.60，试问：

　 (1)3个投保人都能活到75岁的概率；

　 (2)3个投保人中只有1人能活到75岁的概率；

　 (3)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)

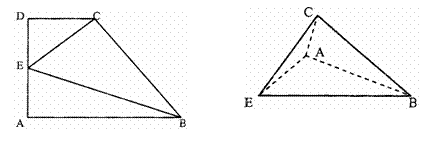
16．一直角梯形ABCD，AB⊥AD，AD⊥DC，AB=2，BC=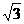，CD=1，E为AD中点，沿

CE、BE把梯形折成四个面都是直角三角形的三棱锥，使点A、D重合，则这三棱锥的

体积等于　　　　　　　 .

15．某学校要从高三的6个班中派9名同学参加市中学生外语口语演讲，每班至少派1人，

则这9个名额的分配方案共有　　　　　　 种.(用数字作答)

14．一个单位有职工360人，其中业务人员276人，管理人员36人，后勤人员48人.为了了解职工的住房情况，要从中抽取一个容量为30的样本，则应该采用　　　　　 　的抽样方法，且应从后勤人员中抽取　　　　 　人.

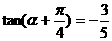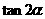13．若则的值是　　　　　　　　　 .

12．13年前有一笔扶贫助学资金，每年的存款利息(年利率11.34%，不扣税)可以资助100

人上学，平均每人每月94.50元。现在(存款年利率1.98%，并且扣20%税)用同样一

笔资金每年的存款利息最多可以资助(　　 )人上学(平均每人每月100元).

A．10　　　　　　　　　　　 B．13　　　　　　　　　　　 C．15　　　　　　　　　　　 D．20

第Ⅱ卷(非选择题)