
题目列表(包括答案和解析)
4.设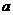 、b、c为三条不同的直线,
、b、c为三条不同的直线,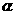 、
、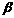 、
、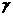 为三个不同的平面,下面四个命题中真命题的个数是 ( )
为三个不同的平面,下面四个命题中真命题的个数是 ( )
①若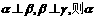 ∥
∥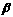 ②若
②若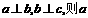 ∥
∥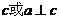 .
.
③若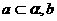 、
、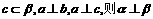 ④若
④若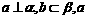 ∥
∥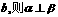
A.1个 B.2个 C.3个 D.4个
3.函数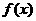 是以
是以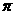 为周期的奇函数,且
为周期的奇函数,且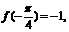 那么
那么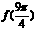 等于 ( )
等于 ( )
A.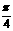 B.-
B.-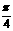 C.1 D.-1
C.1 D.-1
2.若a>b>0,集合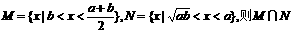 表示的集合为 ( )
表示的集合为 ( )
A.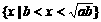 B.
B.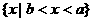
C.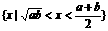 D.
D.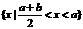
一项是符合题目要求.
1.复数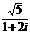 的共轭复数是 ( )
的共轭复数是 ( )
A.1+2i B.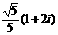 C.1-2i D.
C.1-2i D.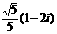
20.(本小题满分14分)
已知:椭圆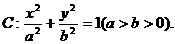
(Ⅰ)若点P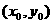 是椭圆C内部一点,求证:
是椭圆C内部一点,求证: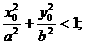
(Ⅱ)若椭圆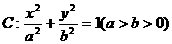 上存在不同的两点关于直线
上存在不同的两点关于直线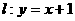 对称,试求
对称,试求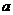 、
、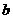 满足的关系式.
满足的关系式.
朝 阳 区 高 三 统 一 练 习(二)
19.(本小题满分14分)
已知: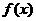 在(-1,1)上有定义,
在(-1,1)上有定义,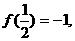 且满足
且满足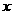 、
、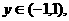 有
有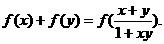
(Ⅰ)求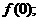
(Ⅱ)证明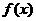 在
在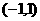 上为奇函数;
上为奇函数;
(Ⅲ)在数列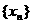 中,
中,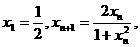 设
设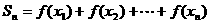 ,求
,求
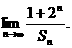
18.(本小题满分14分)
2002年底某县的绿化面积占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
(Ⅰ)设该县的总面积为1,2002年底绿化面积为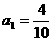 ,经过
,经过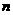 年后绿化的面积为
年后绿化的面积为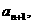 试用
试用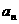 表示
表示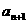 ;
;
(Ⅱ)求数列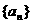 的第
的第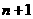 项
项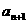 ;
;
(Ⅲ)至少需要多少年的努力,才能使绿化率超过60%.(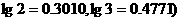
17.(本小题满分14分)
在三棱台ABC-A1B1C1中,侧棱A1A⊥底面ABC,且AC=BC1=2A1C1,
∠BAC=∠BC1C=90°.
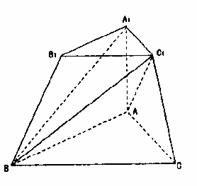 (Ⅰ)求证:CC1⊥平面ABC1;
(Ⅰ)求证:CC1⊥平面ABC1;
(Ⅱ)求AC与BC1所成的角;
(Ⅲ)若A1C1=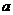 ,求点B1到平面A1C1B的距离.
,求点B1到平面A1C1B的距离.
16.(本小题满分14分)
关于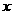 的方程
的方程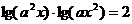 的解都大于1. 求实数
的解都大于1. 求实数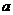 的取值范围.
的取值范围.
15.(本小题满分14分)
设非零复数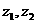 满足
满足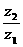 为纯虚数,
为纯虚数,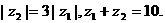 求
求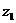 、
、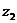 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com