
题目列表(包括答案和解析)
4.若双曲线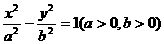 的离心率为2,则双曲线
的离心率为2,则双曲线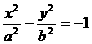 的离心率为
的离心率为
( )
A.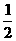 B.
B. C.
C.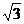 D.2
D.2
3.一个半径为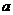 的半球内切于轴截面顶角为
的半球内切于轴截面顶角为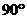 的圆锥,半球的底面在圆锥的底面内,则
的圆锥,半球的底面在圆锥的底面内,则
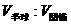 等于 ( )
等于 ( )
A.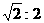 B.2:1 C.2:
B.2:1 C.2: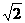 D.1:2
D.1:2
2.若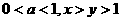 ,下列关系式中不成立的个数是 ( )
,下列关系式中不成立的个数是 ( )
①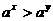 ②
②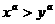
③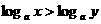 ④
④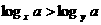
A.4个 B.3个 C.2个 D.1个
只有一项是符合题目要求的。
1.已知全集I={1,2,3,4,5},A∩B={2},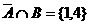 ,则
,则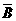 等于 ( )
等于 ( )
A.{3} B.{5} C.{1,2,4} D.{3,5}
(15)(本小题满分14分)
设非零复数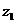 、
、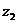 满足
满足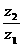 为纯虚数,
为纯虚数,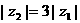 ,
,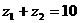 。求
。求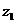 、
、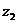 。
。
(16)(本小题满分14分)
关于x的方程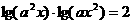 的解都大于1。求实数a的取值范围。
的解都大于1。求实数a的取值范围。
(17)(本小题满分14分)
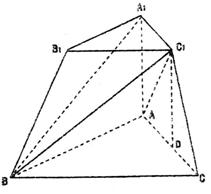
在三棱台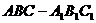 中,侧棱
中,侧棱 ,且
,且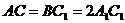 ,
,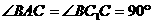 。
。
(I)求证: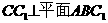 ;
;
(Ⅱ)求AC与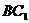 所成的角;
所成的角;
(Ⅲ)若 ,求点
,求点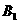 到平面
到平面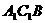 的距离。
的距离。
(18)(本小题满分14分)
2002年底某县的绿化面积占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化。
(I)设该县的总面积为1,2002年底绿化面积为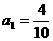 ,经过n年后绿化的面积为
,经过n年后绿化的面积为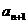 ,试用
,试用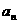 表示
表示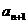 ;
;
(Ⅱ)求数列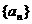 的第n+1项
的第n+1项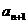 ;
;
(Ⅲ)至少需要多少年的努力,才能使绿化率超过60%。(lg2=0.3010,lg3=0.4771)
(19)(本小题满分14分)
已知:函数f(x)在(-1,1)上有定义,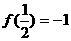 ,且满足x、
,且满足x、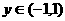 ,有
,有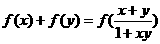 。
。
(I)求f(0);
(Ⅱ)证明f(x)在(-1,1)上为奇函数;
(Ⅲ)在数列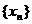 中,
中,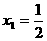 ,
,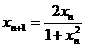 ,设
,设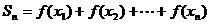 ,求
,求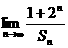 。
。
(20)(本小题满分14分)
已知:椭圆C: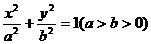 。
。
(I)若点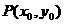 是椭圆C内部的一点,求证:
是椭圆C内部的一点,求证: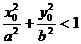 ;
;
(Ⅱ)若椭圆C: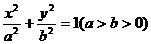 上存在不同的两点关于直线l:y=x+1对称,试求a、b满足的关系式。
上存在不同的两点关于直线l:y=x+1对称,试求a、b满足的关系式。
(11)函数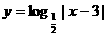 的单调递减区间是_____________。
的单调递减区间是_____________。
(12)圆的极坐标方程是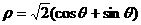 ,该圆的圆心坐标(极坐标)是__________。
,该圆的圆心坐标(极坐标)是__________。
(13)圆锥的轴截面为等边三角形SAB,S为顶点,C是底面圆周上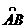 的三等分点,
的三等分点,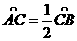 ,则二面角C-SA-B的正切值为_____________。
,则二面角C-SA-B的正切值为_____________。
(14)已知曲线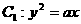 ,与
,与 关于点(1,1)对称的曲线为
关于点(1,1)对称的曲线为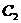 ,且
,且 、
、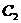 有两个不同的交点,如果过这两个交点的直线的倾斜角为45°,那么实数a的值是___________。
有两个不同的交点,如果过这两个交点的直线的倾斜角为45°,那么实数a的值是___________。
(1)已知全集I={1,2,3,4,5},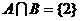 ,
,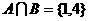 ,则
,则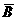 等于
等于
(A){3} (B){5}
(C){1,2,4} (D){3,5}
(2)若0<a<1,x>y>1,下列关系式中不成立的个数是
①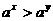 ②
②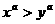
③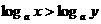 ④
④
(A)4个 (B)3个
(C)2个 (D)1个
(3)一个半径为a的半球内切于轴截面顶角为90°的圆锥,半球的底面在圆锥的底面内,则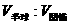 等于
等于
(A)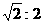 (B)2:1
(B)2:1
(C)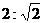 (D)1:2
(D)1:2
(4)若双曲线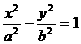 (a>0,b>0)的离心率为2,则双曲线
(a>0,b>0)的离心率为2,则双曲线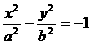 的离心率为
的离心率为
(A)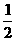 (B)
(B)
(C)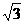 (D)2
(D)2
(5)与函数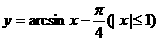 相同的函数是
相同的函数是
(A)
(B)
(C)
(D)
(6)在北纬45°圈上有M、N两地,它们在纬度圈上的弧长是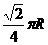 (R是地球的半径),则M、N两地的球面距离为
(R是地球的半径),则M、N两地的球面距离为
(A)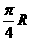 (B)
(B)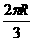
(C)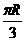 (D)
(D)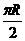
(7)在△ABC中,若tgA=m,tgB=n,且A、B为锐角,那么C为锐角的充要条件是
(A)m>n (B)mn=1
(C)mn<1 (D)mn>1
(8)6个乒乓球运动员,每两个人都可以组成一对双打选手,从中选出两对双打选手的选法有
(A)15种 (B)90种
(C)105种 (D)110种
(9)在数列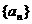 中,
中,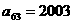 ,
,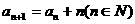 ,则
,则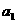 等于
等于
(A)81 (B)50
(C)-13 (D)-46
(10)两游泳者在50米游泳池的对边上同时开始游泳,1人以每秒2.5米、另一人以每秒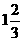 米的速度进行,他们游了4分钟。若不计转向时的时间,则他们迎面闪过的次数为
米的速度进行,他们游了4分钟。若不计转向时的时间,则他们迎面闪过的次数为
(A)7次 (B)8次
(C)9次 (D)10次
第Ⅱ卷(非选择题,共100分)
10.(满分16分)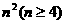 正数排成n行n列
正数排成n行n列

其中每一行的数成等差数列,每一列的数成等比数列,并且所有的公比相等,已知
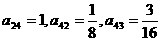 ,求
,求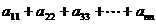 的值。
的值。
9.(满分15分)试问数列
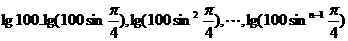 的前多少项的和最大?并求此最大值?
的前多少项的和最大?并求此最大值?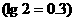 。
。
8.(满分15分)①已知数列 满足
满足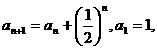 求
求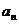 。
。
②已知数列 满足
满足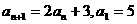 ,求
,求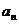 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com