21.(本小题满分12分)

　 在直角坐标平面内，△ABC的两个顶点A，B的坐标分别为A(-1，0)，B(1，0)平面内两点G，M同时满足以下条件：

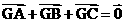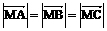　 ①；②；③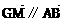

　 (Ⅰ)求△ABC的顶点C的轨迹方程；

　 (Ⅱ)过点P(2，0)的直线l与△ABC的顶点C的轨迹交于E，F两点，求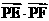的取值范围.

20.(本小题满分12分)

已知a<2，f(x)=(x²+ax+a)e^-x

(Ⅰ)当a=1时，求f(x)的单调区间；

(Ⅱ)是否存在实数a，使f(x)的极大值为3？若存在，求出a的值，若不存在，请说明理由.

19.(本小题满分12分)

　 如图所示，直三棱柱ABC-A₁B₁C₁中，AC=BC=AA₁=2，∠ACB=90°，E为BB₁的中点，点D在AB上且DE=.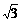

　 (Ⅰ)求证：CD⊥面A₁ABB₁；

　 (Ⅱ)求二面角C-AE-D的大小；

　 (Ⅲ)求点A₁到平面CDE的距离.

18.(本小题满分12分)

甲袋中装有2个白球1个黑球，乙袋中装有3个白球1个红球，现从甲袋中连续三次有放回地摸出一球，从乙袋中连续两次有放回地摸出一球.

(Ⅰ)求从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率；

(Ⅱ)求从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率；

(Ⅲ)设从甲袋中摸出白球的次数为随机变量ζ，求Eζ.

17.(本小题满分12分)

　 已知向量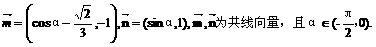

　 (Ⅰ)求sinα-cosα的值；

　 (Ⅱ)求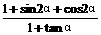的值.

16.将一个四棱锥V-ABCD的每个顶点染上一种颜色，并使每一条棱的两端异色，若只有4种颜色可供使用，则不同的染色方法种数为__________.(用数字作答)

15.如果直线l将圆x²+y²-2x-4y=0平分，且不经过第四象限，那么l的斜率的取值范围是________.

14.为了了解商场某日旅游鞋的销售情况，抽取了

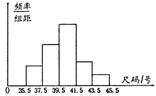部分顾客购鞋的尺寸，将所得的数据整理后，画出

频率分布直方图如图.已知中从左至右前3个小组

的频率之比为1∶2∶3，第4小组与第5小组的

频率分别为0.175和0.075，第二小组的频数为10，则抽取的顾客人数是________.

13.在△ABC中，∠B=30°，AC=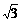，BC=3，则∠C的大小为___________.

12.一个机器人每一秒钟前进一步或后退一步，程序设计师设计的程序是让机器人以先前进3步，然后再后退2步的规律移动，如果将机器人放在数轴的原点，面向正的方向在数轴上移动(1步的距离为1个单位长度).令P(n)表示第n秒时机器人所在位置的坐标，且记P(0)=0,则下列结论中错误的是

　 A.P(3)=3　　　 B.P(5)=1　　 　 C. P (2007)>P(2006)　 　　 D.P(2003)<P(2006)

第Ⅱ卷(非选择题　　 　 共90分)