
题目列表(包括答案和解析)
4. 已知l、m为两条不重合的直线,α、β为两个不重合的平面,则下列条件中可以判断平面α与平面β平行的是
A.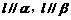 B.
B.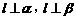 C.
C.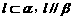 D.
D.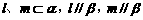
3. 若命题P:x∈A∩B,则命题非P是
A.x∈A∪B B.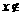 A∪B C.x
A∪B C.x A或x
A或x B D.x
B D.x A且x
A且x B
B
2. 函数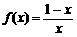 的反函数为
的反函数为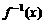 ,若
,若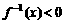 ,则x的取值范围是
A.(-∞,0) B.(-1,1) C.(1,+∞) D.(-∞,-1)
,则x的取值范围是
A.(-∞,0) B.(-1,1) C.(1,+∞) D.(-∞,-1)
1. “两条直线没有公共点”是“这两条直线异面”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
22.(1)设Q(x,y),∵p、Q两点关于原点对称,∴p点的坐标为(-x,-y),又点p(-x,-y)在函数y=f(x)的图象上,∴-y=loga(-x+1),即g(x)=-loga(1-x)………………(2分)
(2)由2f(x)+g(x)≥0得2loga(x+1)≥loga(1-x)
∵0<a<1 ∴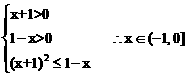 ……………………………………(6分)
……………………………………(6分)
(3)由题意知:a>1且x∈[0,1)时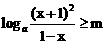 恒成立。……………(7分)
恒成立。……………(7分)
设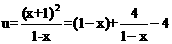 ,令t=1-x,t∈(0,1],∴
,令t=1-x,t∈(0,1],∴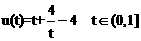
………………………………………………………………………………………(9分)
设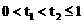
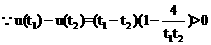
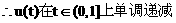 ,
,
∴u(t)的最小值为1…………………………………………………………………(12分)
又∵a>1,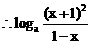 的最小值为0…………………………………………(13分)
的最小值为0…………………………………………(13分)
∴m的取值范围是m≤0……………………………………………………………(14


21.(本小题满分12分)
解(I)逆命题:在等比数列{an}中,前n项和为Sn,若a2 , a4, a3成等差数列,则S2,S4,S3成等差数列 ………………………………3分
(II)设{an}的首项为a1,公比为q
由已知得2a4= a2 + a3 ∴2a1q3=a1q+a1q2
∵a1≠0 q≠0 ∴2q2-q-1=0 ∴q=1或q=-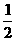 ……………………5分
……………………5分
当q=1时,S2=2a1, S4=4 a1,S3=3 a1,
∴S2+S3≠2 S4 ∴S2,S4,S3不成等差数列 ………………………………7分
当q=-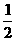 时
时
S2+S3=(a1+a2)+( a1+a2+a3)=2[a1+a1×(-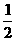 )]+a1(-
)]+a1(-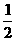 )2=
)2=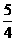 a1
a1
2 S4=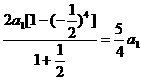
∴S2+S3=2 S4 ∴S2,S4,S3成等差数列 ………………………………10分
综上得:当公比q=1时,逆命题为假
当公比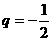 时,逆命题为真 ……………………………………12分
时,逆命题为真 ……………………………………12分
19.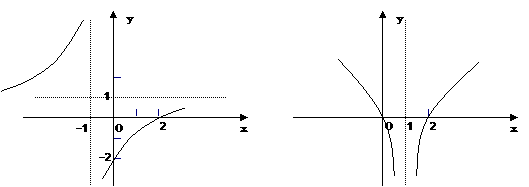 解:(1)
解:(1)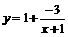 (2)
(2)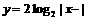
(1) (2)
20(1)解:A={x|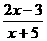 ≤0}={x|-5<x≤
≤0}={x|-5<x≤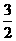 }……………………1分
}……………………1分
B={x|x2-3x+2<0}={x|1<x<2}…………………………2分
(Ⅰ)A∪B={x|-5<x<2}………………………………4分
(Ⅱ)(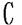 uA)={x|x≤-5或x>
uA)={x|x≤-5或x>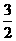 } (
} (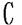 uA)∩B={x|
uA)∩B={x|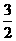 <x<2}……6分
<x<2}……6分
(2)解: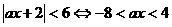 ………………………………1分
………………………………1分
当a=0时,原不等式的解集为R,与题设不符(舍去) …………………2分
当a>0时,有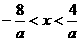 ,而已知原不等式的解集为
,而已知原不等式的解集为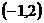 ,所以有:
,所以有:
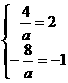 此方程无解(舍去) ………………………………3分
此方程无解(舍去) ………………………………3分
当a<0时,有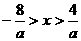 ,所以有:
,所以有: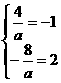 解得a=-4………………… 5分
解得a=-4………………… 5分
故所求a=-4. ………………………………………………………………6分
18.解: 数列
数列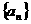 成等差数列,
成等差数列,
 ……………………………2分
……………………………2分

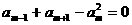

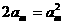
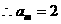 或
或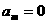 ……6分
……6分
由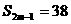 得:
得:
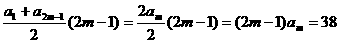 ………………10分
………………10分
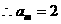 ,代入上式得:
,代入上式得: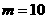 ……………………………12分
……………………………12分
17. 解:∵原式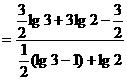 ………………5分(每化简一个得1分)
………………5分(每化简一个得1分)
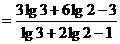 ………………6分
………………6分
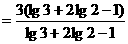 ………………7分
………………7分
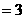 ………………8分
………………8分
16. 1≤m<2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com