
题目列表(包括答案和解析)
2.数列的求和
等差数列与等比数列的有限项求和总是有公式可求的,其它的数列的求和不总是可求的,但某些特殊数列的求和可采用分部求和法转化为等差数列或等比数列的和或用裂项求和法、错位相减法、逆序相加法、组合化归法,递推法。
① 分部求和法
例1.
已知等差数列 的首项为1,前10项的和为145,求
的首项为1,前10项的和为145,求
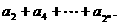
解析:首先由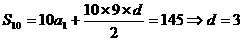
则:
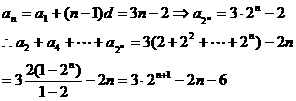
② 裂项求和法
例2. 已知数列 为等差数列,且公差不为0,首项也不为0,
为等差数列,且公差不为0,首项也不为0,
求和: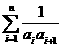 。
。
解析:首先考虑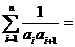
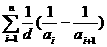
则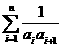 =
=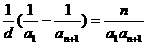
点评:已知数列 为等差数列,且公差不为0,首项也不为0,下列求和
为等差数列,且公差不为0,首项也不为0,下列求和
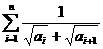 也可用裂项求和法。
也可用裂项求和法。
③ 错位相减法
例3.已知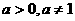 ,数列
,数列 是首项为a,公比也为a的等比数列,令
是首项为a,公比也为a的等比数列,令
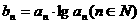 ,求数列
,求数列 的前
的前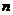 项和
项和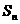 。
。
解析:
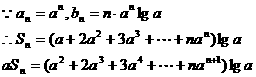
①-②得: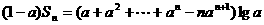
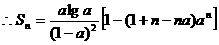 。
。
点评:设数列 的等比数列,数列
的等比数列,数列 是等差数列,则数列
是等差数列,则数列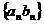
的前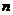 项和
项和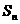 求解,均可用错位相减法。
求解,均可用错位相减法。
④ 组合化归法
例4.求和:
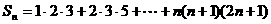 。
。
解析: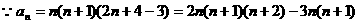
而连续自然数可表示为组合数的形式,于是,数列的求和便转化为组合数的
求和问题了。
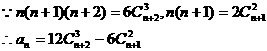
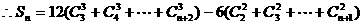
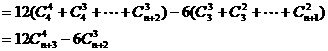
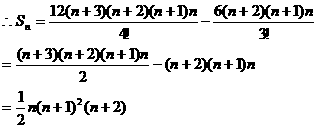
点评:可转化为连续自然数乘积的数列求和问题,均可考虑组合化归法。
⑤ 逆序相加法
例5.设数列 是公差为
是公差为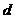 ,且首项为
,且首项为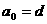 的等差数列,求和:
的等差数列,求和:
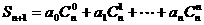
解析:因为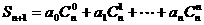
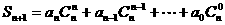
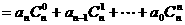
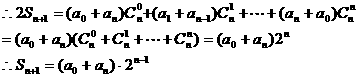
点评:此类问题还可变换为探索题形:
已知数列 的前
的前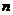 项和
项和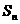
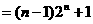 ,是否存在等差数列
,是否存在等差数列 使得
使得
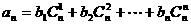 对一切自然数n都成立。
对一切自然数n都成立。
⑥ 递推法
例6. 已知数列 的前
的前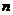 项和
项和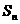 与
与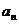 满足:
满足: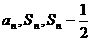
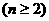 成
成
等比数列,且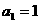 ,求数列
,求数列 的前
的前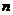 项和
项和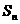 。
。
解析:由题意: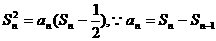
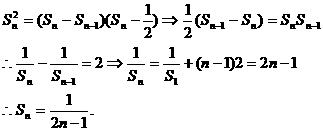
点评:本题的常规方法是先求通项公式,然后求和,但逆向思维,直接求出数列 的前
的前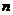 项和
项和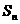 的递推公式,是一种最佳解法。
的递推公式,是一种最佳解法。
5.化归法
例5. 已知数列 中,
中,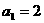 ,
,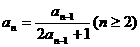 ,
,
求通项公式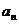 。
。
解析:倒数化归得: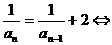
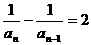
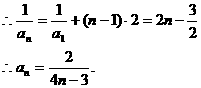
点评:常用的化归还有对数化归,待定化归,一般需转化为等比数列或等差数列的问题。如例1中的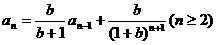 可转化为
可转化为
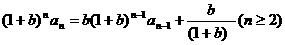
令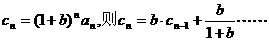 ①
①
问题①的解决可用待定系数法或特征根法。
⑥ 待定系数法
对于由一阶、二阶或 三阶的线性递推公式求通项问题,均可用待定系数法。
例6. 已知数列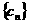 中,
中,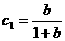 ,
,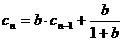 ,
,
其中b是与n无关的常数,且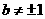 。求出用n和b表示的an的关系式。
。求出用n和b表示的an的关系式。
解析:递推公式一定可表示为
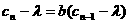 的形式。
的形式。
由待定系数法知:
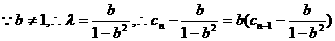

故数列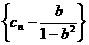 是首项为
是首项为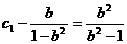 ,公比为
,公比为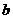 的
的
等比数列,故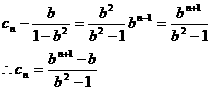
4.叠乘法
例4. 已知数列 中,
中,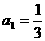 ,前
,前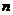 项和
项和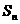 与
与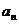 的关系是
的关系是
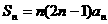 ,试求通项公式
,试求通项公式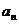 。
。
解析:首先由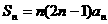 易求的递推公式:
易求的递推公式:
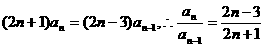
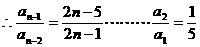
将上面n-1个等式相乘得:
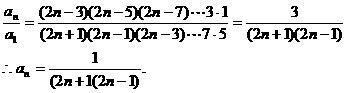
3.阶差法
例3.(本专题例1)已知数列 的前
的前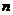 项和
项和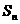 与
与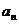 的关系是
的关系是
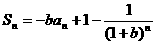 ,其中b是与n无关的常数,且
,其中b是与n无关的常数,且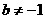 。
。
求出用n和b表示的an的关系式。
解析:首先由公式: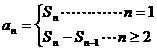 得:
得:
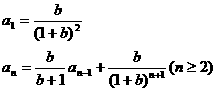
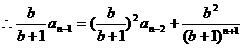
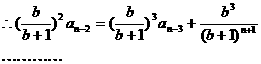
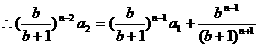
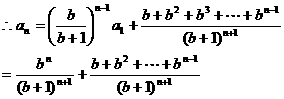
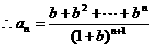
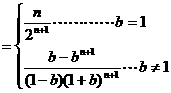
点评:利用阶差法要注意:递推公式中某一项的下标与其系数的指数的关系,即
其和为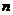 。
。
1. 求数列的通项的方法
求数列的通项的常用方法有观察法-归纳-证明法、公式法、阶差法、叠乘法、化归法、
待定系数法、特征方程法。
①.归纳-猜测-证明法
由题设条件求出数列的前几项,然后归纳出一般表达式,形成猜想,然后用数学归纳法加以证明,得出正确的结论,是一种重要的思维方法。
例1.已知数列 的前
的前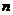 项和
项和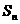 与通项
与通项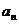 的关系是
的关系是
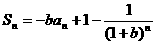 ,其中b是与n无关的常数,且
,其中b是与n无关的常数,且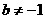 。
。
求出用n和b表示的an的关系式。
解析:首先由公式: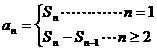 得:
得:
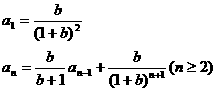

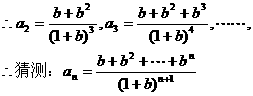
其次,用数学归纳法证明。证明略。
②.公式法
若已知数列的前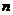 项和
项和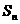 与
与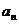 的关系,求数列
的关系,求数列 的通项
的通项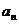 可用公式
可用公式
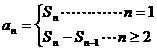 求解。
求解。
例2. 设数列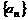 的首项为a1=1,前n项和Sn满足关系
的首项为a1=1,前n项和Sn满足关系
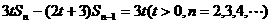
求证:数列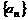 是等比数列。
是等比数列。
解析:因为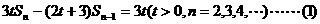
所以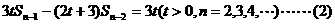
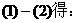
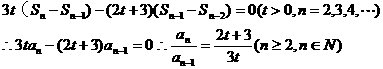 所以,数列
所以,数列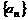 是等比数列。
是等比数列。
点评:公式的应用要灵活,如本例。
2. 掌握数列求和的方法。
1. 掌握数列通项的求法。
22.(14分)设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x, y,均有
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(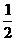 )的值;
)的值;
(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M·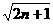 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
21.(12分)设数列{an}的前n项和为Sn,已知a1=1,且满足3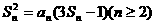
(1)求证: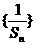 为等差数列
为等差数列
(2)设
20.(12分)某家用电器厂根据其产品在市场上的销售情况,决定对原来以每件2000元出售的一种产品进行调价,并按新单价的八折优惠销售。结果每件产品仍可获得实际销售价20%的利润。已知该产品每件的成本是原销售价的60%。
(1)求调价后这种产品的新单价是每件多少元?让利后的实际销售价是每件多少元?
(2)为使今年按新单价让利销售后的利润总额不低于20万元,今年至少应销售这种产品多少件?(每件产品利润=每件产品的实际销售价一每件产品的成本价)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com