
题目列表(包括答案和解析)
2. (北京卷)已知n次多项式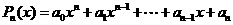 ,
,
如果在一种算法中,计算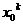 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算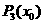 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算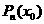 的值共需要
的值共需要  n(n+3)
次运算.
n(n+3)
次运算.
下面给出一种减少运算次数的算法: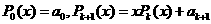 (k=0, 1,2,…,n-1).利用该算法,计算
(k=0, 1,2,…,n-1).利用该算法,计算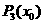 的值共需要6次运算,计算
的值共需要6次运算,计算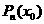 的
的
值共需要 2n 次运算.
1. (广东卷)
设平面内有n条直线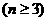 ,其中有且仅有两条直线互相平行,任意三角形不过同一点.若用
,其中有且仅有两条直线互相平行,任意三角形不过同一点.若用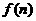 表示这n条直线交点的个数,则
表示这n条直线交点的个数,则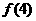 _____5________;当n>4时,
_____5________;当n>4时,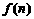 =__
=__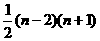 ___________.
___________.
13. (江西卷)
填空题
12.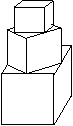 (重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( C)
(重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( C)
(A) 4;
(B) 5;
(C) 6;
(D) 7。
11. (浙江卷)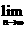
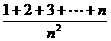 =( C )
=( C )
(A) 2 (B) 4 (C)  (D)0
(D)0
10. (上海)16.用n个不同的实数a1,a2,┄an可得n!个不同的排列,每个排列为一行写成 1 2 3
一个n!行的数阵.对第i行ai1,ai2,┄ain,记bi=- ai1+2ai2-3 ai3+┄+(-1)nnain, 1 3 2
i=1,2,3, ┄,n!.用1,2,3可你数阵如右,由于此数阵中每一列各数之和都 2 1 3
是12,所以,b1+b2+┄+b6=-12+2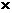 12-3
12-3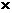 12=-24.那么,在用1,2,3,4,5形成 2 3 1
12=-24.那么,在用1,2,3,4,5形成 2 3 1
的数阵中, b1+b2+┄+b120等于 3 1 2
3 2 1
[答]( C )
(A)-3600 (B) 1800 (C)-1080 (D)-720
9. (山东卷)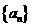 是首项
是首项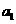 =1,公差为
=1,公差为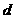 =3的等差数列,如果
=3的等差数列,如果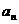 =2005,则序号
=2005,则序号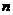 等于(C )
等于(C )
(A)667 (B)668 (C)669 (D)670
8. (全国卷II) 11如果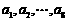 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差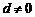 ,则(B)
,则(B)
(A)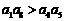 (B)
(B)
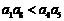 (C)
(C)
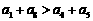 (D)
(D) 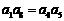
7. (全国卷II) 如果数列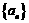 是等差数列,则(B )
是等差数列,则(B )
(A)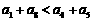 (B)
(B)
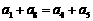 (C)
(C) 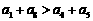 (D)
(D) 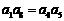
6. (江苏卷)在各项都为正数的等比数列{an}中,首项a1=3 ,前三项和为21,则a3+ a4+ a5=(C )
( A ) 33 ( B ) 72 ( C ) 84 ( D )189
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com