
题目列表(包括答案和解析)
7.(天津卷)在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),若点C在∠AOB的平分线上且|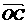 |=2,则
|=2,则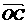 =
=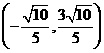
6.(上海卷)直角坐标平面 中,若定点
中,若定点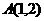 与动点
与动点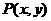 满足
满足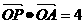 ,则点P的轨迹方程是x+2y-4=0 __________。
,则点P的轨迹方程是x+2y-4=0 __________。
5.(北京卷)若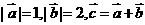 ,且
,且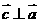 ,则向量
,则向量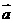 与
与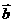 的夹角为(C )
的夹角为(C )
(A)30° (B)60° (C)120° (D)150°
4. (全国卷III)已知向量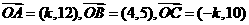 ,且A、B、C三点共线,则k=
,且A、B、C三点共线,则k=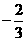
3.(全国卷Ⅱ)点P在平面上作匀速直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为 ( C )
A.(-2,4) B.(-30,25) C.(10,-5) D.(5,-10)
2.(全国卷Ⅱ)已知点A(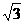 ,1),B(0,0)C(
,1),B(0,0)C(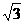 ,0).设∠BAC的平分线AE与BC相交于E,那么有
,0).设∠BAC的平分线AE与BC相交于E,那么有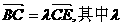 等于 ( C )
等于 ( C )
A.2 B.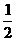 C.-3 D.-
C.-3 D.-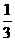
1.(全国卷Ⅰ)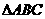 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H,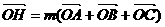 ,则实数m = 1
,则实数m = 1
22.(本题满分18分)
已知函数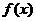 是定义在
是定义在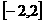 上的奇函数,当
上的奇函数,当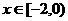 时,
时,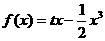 (
(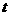 为常数)。
为常数)。
(1)求函数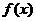 的解析式;
的解析式;
(2)当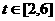 时,求
时,求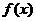 在
在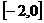 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的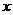 ,并猜想
,并猜想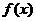 在
在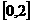 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当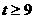 时,证明:函数
时,证明:函数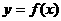 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线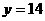 上。
上。
解:(1)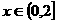 时,
时,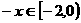 , 则
, 则 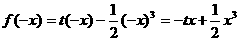
∵函数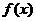 是定义在
是定义在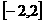 上的奇函数,即
上的奇函数,即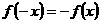
∴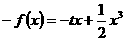 ,即
,即 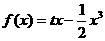 ,又可知
,又可知 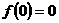
∴函数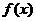 的解析式为
的解析式为 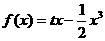 ,
,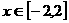
(2)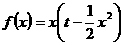 ,∵
,∵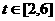 ,
,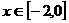 ,∴
,∴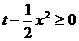
∵ 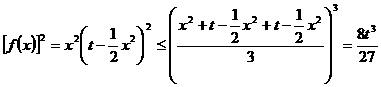
∴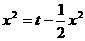 ,即
,即 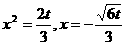
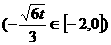 时,
时,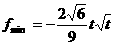 。
。
猜想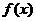 在
在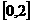 上的单调递增区间为
上的单调递增区间为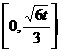 。
。
(3)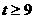 时,任取
时,任取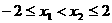 ,∵
,∵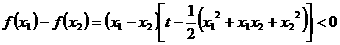
∴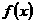 在
在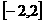 上单调递增,即
上单调递增,即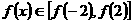 ,即
,即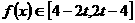
∵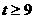 ,∴
,∴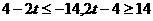 ,∴
,∴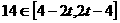
∴当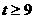 时,函数
时,函数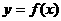 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线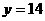 上。
上。
21.(本题满分16分)
对数列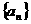 ,规定
,规定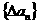 为数列
为数列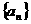 的一阶差分数列,其中
的一阶差分数列,其中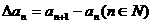 。
。
对自然数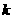 ,规定
,规定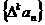 为
为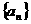 的
的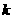 阶差分数列,其中
阶差分数列,其中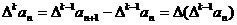 。
。
(1)已知数列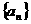 的通项公式
的通项公式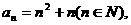 ,试判断
,试判断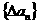 ,
,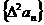 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列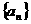 首项
首项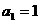 ,且满足
,且满足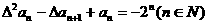 ,求数列
,求数列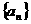 的通项公式。
的通项公式。
(3)对(2)中数列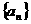 ,是否存在等差数列
,是否存在等差数列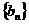 ,使得
,使得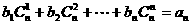 对一切自然
对一切自然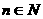 都成立?若存在,求数列
都成立?若存在,求数列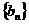 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
解:(1)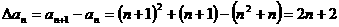 ,∴
,∴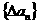 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
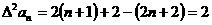
∴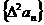 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)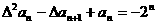 ,即
,即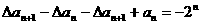 ,即
,即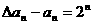 ,∴
,∴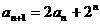
∵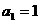 ,∴
,∴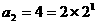 ,
,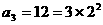 ,
,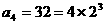 ,猜想:
,猜想: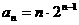
证明:ⅰ)当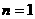 时,
时,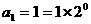 ;
;
ⅱ)假设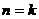 时,
时,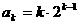
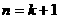 时,
时,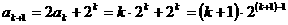 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,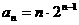
(3)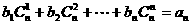 ,即
,即 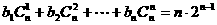
∵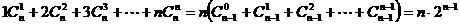
∴存在等差数列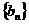 ,
,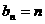 ,使得
,使得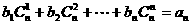 对一切自然
对一切自然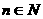 都成立。
都成立。
20.(本题满分14分)
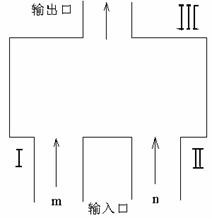 如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数
如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数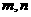 时,输出结果记为
时,输出结果记为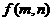 ,且计算装置运算原理如下:
,且计算装置运算原理如下:
①
若Ⅰ、Ⅱ分别输入1,则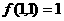 ;②若Ⅰ输入固定的正整数,
;②若Ⅰ输入固定的正整数,
Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,
Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:
(1)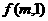 的表达式
的表达式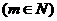 ;(2)
;(2)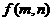 的表达式
的表达式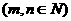 ;
;
(3)若Ⅰ、Ⅱ都输入正整数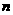 ,则输出结果
,则输出结果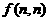 能否为2005?
能否为2005?
若能,求出相应的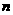 ;若不能,则请说明理由。
;若不能,则请说明理由。
解:(1)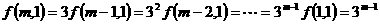
(2)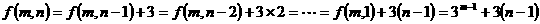
(3)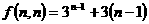 ,∵
,∵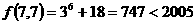 ,
,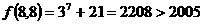
∴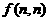 输出结果不可能为
输出结果不可能为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com