
题目列表(包括答案和解析)
在曲线上两点关于某直线对称问题,分三步:求两点所在的直线,求这两直线的交点,使这交点在圆锥曲线形内。
例4 已知椭圆C的方程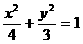 ,试确定m的取值范围,使得对于直线
,试确定m的取值范围,使得对于直线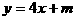 ,椭圆C上有不同两点关于直线对称。
,椭圆C上有不同两点关于直线对称。
分析:椭圆上两点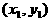 ,
,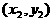 ,代入方程,相减得
,代入方程,相减得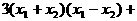
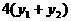
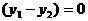 。
。
又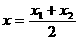 ,
,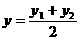 ,
, ,代入得
,代入得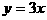 。
。
又由 解得交点
解得交点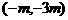 。
。
交点在椭圆内,则有
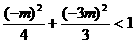 。
。
得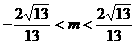 。
。
例5 为了使抛物线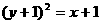 上存在两点关于直线
上存在两点关于直线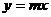 对称,求m的取值范围。
对称,求m的取值范围。
略解:两点所在直线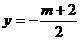 与
与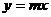 联立求出交点
联立求出交点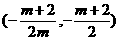 ,代入抛物线内,有
,代入抛物线内,有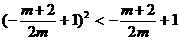 ,解得
,解得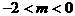 。
。
椭圆或双曲线上一点P,与两个焦点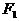 、
、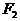 构成的三角形问题,常用正、余弦定理搭桥。
构成的三角形问题,常用正、余弦定理搭桥。
例3 设P(x,y)为椭圆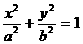 上任一点,
上任一点,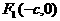 ,
,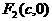 为焦点,
为焦点,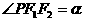 ,
,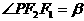 。
。
(1)求证离心率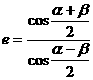 ;
;
(2)求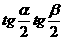 的值;
的值;
(3)求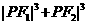 的最值。
的最值。
分析:(1)设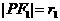 ,
,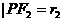 ,由正弦定理得
,由正弦定理得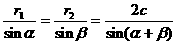 。
。
得 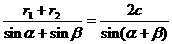 ,
,
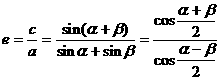 。
。
(2)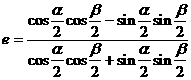 ,采用合分比定理得
,采用合分比定理得
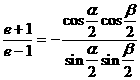 ,
,
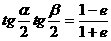 。
。
(3)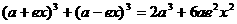 。
。
当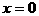 时,最小值是
时,最小值是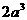 ;
;
当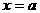 时,最大值是
时,最大值是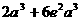 。
。
具有斜率的弦中点问题,一般设曲线上两点为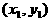 ,
,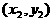 ,代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数。
,代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数。
例1 给定双曲线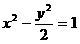 。过A(2,1)的直线与双曲线交于两点
。过A(2,1)的直线与双曲线交于两点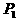 及
及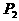 ,求线段
,求线段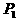
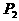 的中点P的轨迹方程。
的中点P的轨迹方程。
分析:设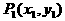 ,
,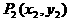 代入方程得
代入方程得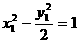 ,
,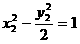 。
。
两式相减得
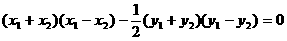 。
。
又设中点P(x,y),将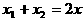 ,
,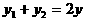 代入,当
代入,当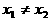 时得
时得
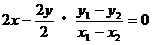 。
。
又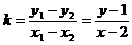 ,
,
代入得 。
。
当弦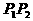 斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程是
斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程是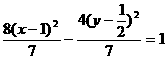 。
。
例2 已知椭圆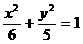 ,通过点(1,1)引一弦,使它在这点被平分,求此弦所在的直线方程。
,通过点(1,1)引一弦,使它在这点被平分,求此弦所在的直线方程。
略解:有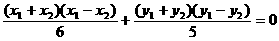 ,代入得
,代入得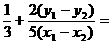
0,得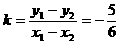 。
。
从而直线方程是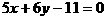 。
。
此题将椭圆变为双曲线、抛物线都是同一方法。
22.(本小题满分14分)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
⑴如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
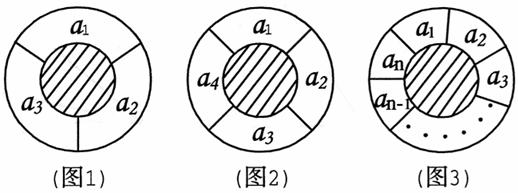 ⑵如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
⑵如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
21.(本小题满分12分)当n∈N且n>1时,求证2<(1+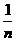 )n<3。
)n<3。
20.(本小题满分12分)规定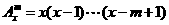 ,其中x∈R,m为正整数,且
,其中x∈R,m为正整数,且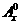 =1,这是排列数
=1,这是排列数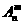 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
⑴求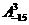 的值;
的值;
⑵排列数的两个性质:①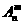 =n
=n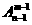 , ②
, ②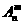 +m
+m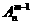 =
=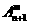 .(其中m,n是正整数)是否都能推广到
.(其中m,n是正整数)是否都能推广到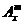 (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
⑶确定函数 的单调区间.
的单调区间.
19.(本小题满分12分)二项式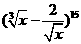 的展开式中:
的展开式中:
⑴求常数项;
⑵有几个有理项;
⑶有几个整式项。
18.(本小题满分12分)某人手中有5张扑克牌,其中2张为不同花色的2,3张为不同花色的A,他有5次出牌机会,每次只能出一种点数的牌,但张数不限,此人有多少种不同的出牌方法?
17.(本小题满分12分)某学习小组有8个同学,从男生中选2人,女生中选1人参加数学、物理、化学三种竞赛,要求每科均有1人参加,共有180种不同的选法,那么该小组中男、女同学各有多少人?
16.关于二项式(x-1)2005有下列命题:
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为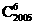 x1999;
x1999;
③该二项展开式中系数最大的项是第1002项;
④当x=2006时,(x-1)2005除以2006的余数是2005。
其中正确命题的序号是 。(注:把你认为正确的命题序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com