
题目列表(包括答案和解析)
8.设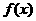 、
、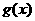 都是定义在
都是定义在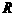 上的奇函数,不等式
上的奇函数,不等式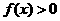 的解集为
的解集为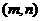 ,不等式
,不等式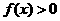 的解集为
的解集为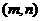 ,不等式
,不等式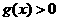 的解集为
的解集为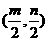 ,其中
,其中 ,则不等式
,则不等式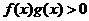 的解集为( )
的解集为( )
(A) 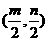 (B)
(B)
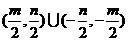
(C) 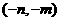 (D)
(D) 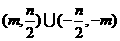
7.若关于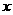 的不等式
的不等式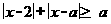 在R上恒成立,则
在R上恒成立,则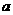 的最大值是( )
的最大值是( )
(A)0 (B)1 (C)-1 (D)2
6.若不等式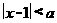 成立的充分条件是
成立的充分条件是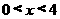 ,则
,则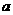 的取值范围是( )
的取值范围是( )
(A)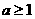 (B)
(B)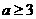 (C)
(C)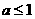 (D)
(D)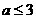
5.若实数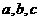 满足
满足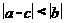 ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )
(A)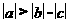 (B)
(B)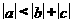 (C)
(C)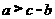 (D)
(D)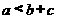
4.设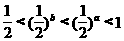 ,则( )
,则( )
(A)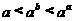 (B)
(B)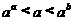 (C)
(C)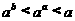 (D)
(D)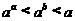
3.不等式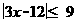 的整数解的个数是( )
的整数解的个数是( )
(A)7 (B)6 (C)5 (D)4
2.不等式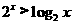 的解集是( )
的解集是( )
(A)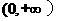 (B)
(B)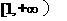 (C)R (D)ф
(C)R (D)ф
1.不等式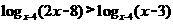 的解集是( )
的解集是( )
(A)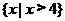 (B)
(B)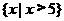
(C)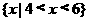 (D)
(D)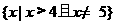
25. (江西卷)
已知数列
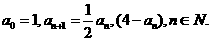
(1)证明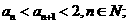
(2)求数列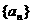 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,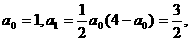
∴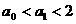 ,命题正确.
,命题正确.
2°假设n=k时有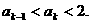
则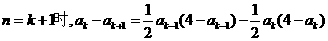
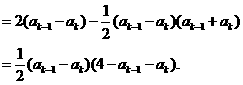
而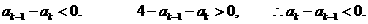
又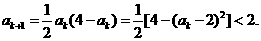
∴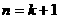 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有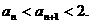
方法二:用数学归纳法证明:
1°当n=1时,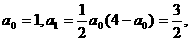 ∴
∴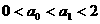 ;
;
2°假设n=k时有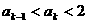 成立,
成立,
令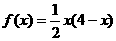 ,
,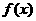 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: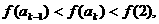 即
即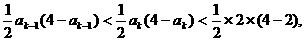
也即当n=k+1时 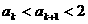 成立,所以对一切
成立,所以对一切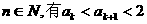
(2)下面来求数列的通项: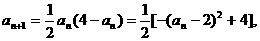 所以
所以
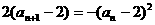
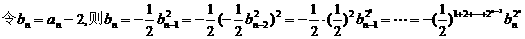 ,
,
又bn=-1,所以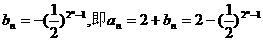
24. (江西卷)已知数列{an}的前n项和Sn满足Sn-Sn-2=3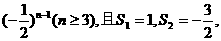 求数列{an}的通项公式.
求数列{an}的通项公式.
解:方法一:先考虑偶数项有: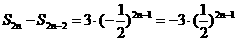

………
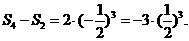
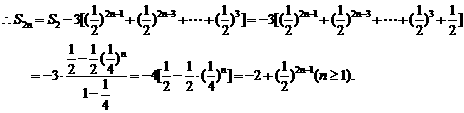
同理考虑奇数项有: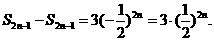
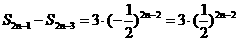
………
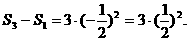
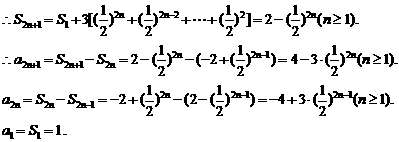
综合可得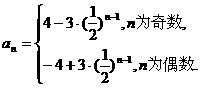
方法二:因为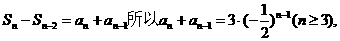
两边同乘以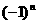 ,可得:
,可得:
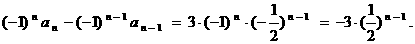
令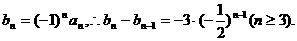
所以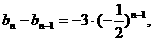
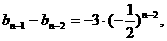
………
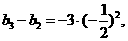
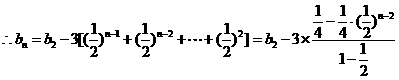
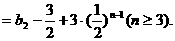
又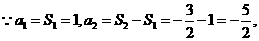
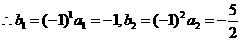
∴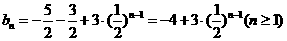
∴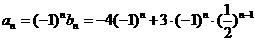
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com