
题目列表(包括答案和解析)
5.(天津卷)将直线2x-y+λ=0,沿x轴向左平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为
A.-3或7 B.-2或8 C.0或10 D.1或11
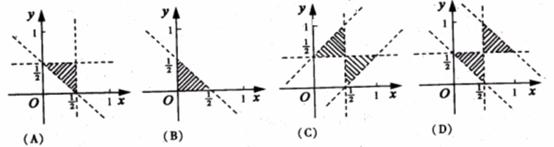
5.(浙江)设集合A={(x,y)|x,y,1-x-y是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是( A )
3. (重庆卷)圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为 (A )
(A) (x-2)2+y2=5; (B) x2+(y-2)2=5;
(C) (x+2)2+(y+2)2=5; (D) x2+(y+2)2=5。
4 (浙江)点(1,-1)到直线x-y+1=0的距离是( D )
(A) 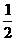 (B)
(B) 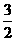 (C)
(C) 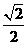 (D)
(D)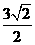
2.(江西卷) “a=b”是“直线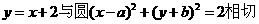 ”的 (A )
”的 (A )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
1.(江西卷)在△OAB中,O为坐标原点,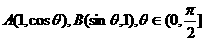 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,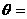 ( D
)
( D
)
A.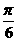 B.
B.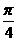 C.
C.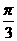 D.
D.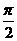
24.(江苏卷)已知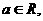 函数
函数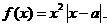
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
解:(1)当a=2时,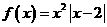 ,则方程f(x)=x即为
,则方程f(x)=x即为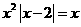
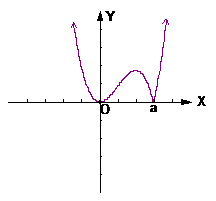
解方程得: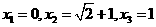
(2)(I)当a>0时,
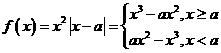 ,
,
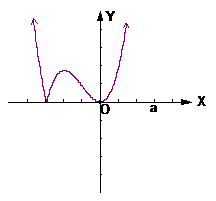
作出其草图见右, 易知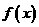 有两个极值点
有两个极值点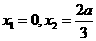 借助于图像可知
借助于图像可知
当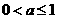 时,函数
时,函数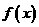 在区间[1,2]上为增函数,此时
在区间[1,2]上为增函数,此时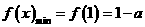
当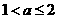 时,显然此时函数的最小值为
时,显然此时函数的最小值为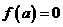
当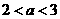 时,
时,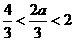 ,此时
,此时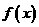 在区间
在区间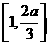 为增函数,在区间
为增函数,在区间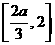 上为减函数,∴
上为减函数,∴ ,又可得
,又可得
∴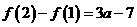
则当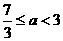 时,
时,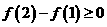 ,此时
,此时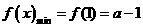
当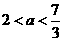 时,
时,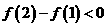 ,此时
,此时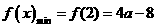
当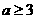 时,
时,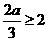 ,此时
,此时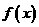 在区间
在区间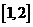 为增函数,故
为增函数,故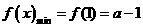
(II)当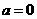 时,
时,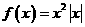 ,此时
,此时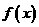 在区间
在区间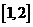 也为增函数,故
也为增函数,故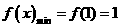
(III)当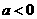 时,其草图见右
时,其草图见右
显然函数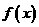 在区间
在区间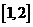 为增函数,故
为增函数,故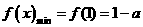
19.(本小题13分)
解: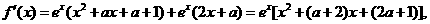
令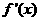 =0得
=0得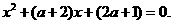
(1)当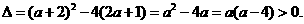
即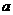 <0或
<0或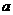 >4时
>4时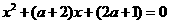 有两个不同的实根
有两个不同的实根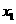 ,
,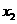 ,不妨设
,不妨设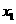 <
<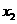
于是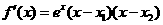 ,从而有下表
,从而有下表
|
x |
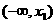 |
x1 |
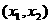 |
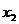 |
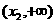 |
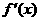 |
+ |
0 |
- |
0 |
+ |
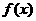 |
↑ |
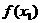 为极大值 为极大值 |
↓ |
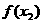 为极小值 为极小值 |
↑ |
即此时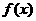 有两个极值点.
有两个极值点.
(2)当△=0即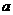 =0或
=0或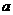 =4时,方程
=4时,方程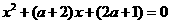 有两个相同的实根
有两个相同的实根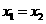
于是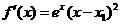
故当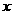 <
<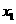 时
时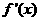 >0,当
>0,当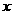 >
>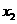 时
时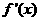 >0,因此
>0,因此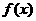 无极值
无极值
(3)当△<0即0<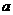 <4时
<4时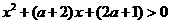
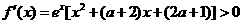 ,故
,故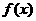 为增函数,此时
为增函数,此时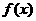 无极值. 因此当
无极值. 因此当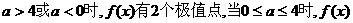 无极值点.
无极值点.
23. (重庆卷)已知aÎR,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数。
22.(重庆卷)设函数f(x)=2x3-3(a+1)x2+6ax+8,其中aÎR。
(1) 若f(x)在x=3处取得极值,求常数a的值;
(2) 若f(x)在(-¥,0)上为增函数,求a的取值范围。
解:(Ⅰ)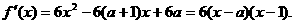
因 取得极值, 所以
取得极值, 所以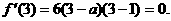 解得
解得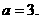
经检验知当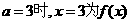 为极值点.
为极值点.
(Ⅱ)令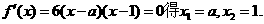
当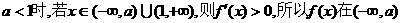 和
和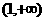 上为增函数,故当
上为增函数,故当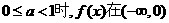 上为增函数.
上为增函数.
当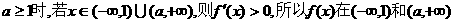 上为增函数,从而
上为增函数,从而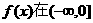 上也为增函数.
上也为增函数.
综上所述,当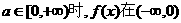 上为增函数.
上为增函数.
21. (山东卷)已知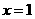 是函数
是函数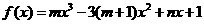 的一个极值点,其中
的一个极值点,其中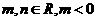 ,
,
(I)求 与
与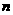 的关系式;
的关系式;
(II)求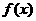 的单调区间;
的单调区间;
(III)当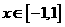 时,函数
时,函数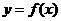 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
解(I)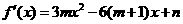 因为
因为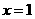 是函数
是函数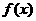 的一个极值点,所以
的一个极值点,所以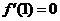 ,即
,即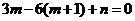 ,所以
,所以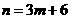
(II)由(I)知,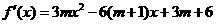 =
=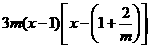
当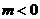 时,有
时,有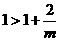 ,当
,当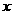 变化时,
变化时,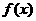 与
与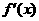 的变化如下表:
的变化如下表:
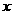 |
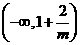 |
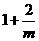 |
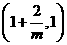 |
1 |
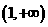 |
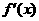 |
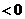 |
0 |
 |
0 |
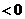 |
|
|
|
|
|
|
|
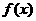 |
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当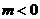 时,
时,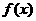 在
在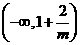 单调递减,在
单调递减,在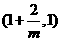 单调递增,在
单调递增,在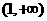 上单调递减.
上单调递减.
(III)由已知得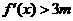 ,即
,即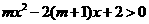
又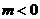 所以
所以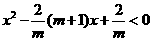 即
即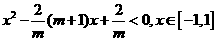 ①
①
设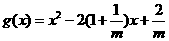 ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以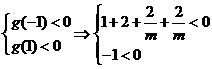 解之得
解之得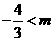 又
又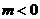 所以
所以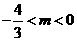
即 的取值范围为
的取值范围为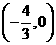
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com