
题目列表(包括答案和解析)
1. 过抛物线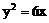 的焦点F,作弦
的焦点F,作弦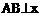 轴于A、B两点,则弦长
轴于A、B两点,则弦长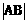 等于( )
等于( )
A. 6 B. 18 C. 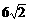 D. 36
D. 36
21.根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在的两定点,使得点P到两点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)设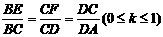
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak)直线OF的方程为: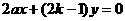 ①
①
直线GE的方程为: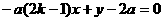 ②
②
从①,②消去参数k,得点P(x,y)坐标满足方程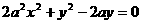
整理得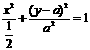 当
当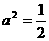 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当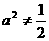 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
当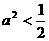 时,点P到椭圆两个焦点(
时,点P到椭圆两个焦点(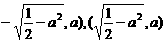 的距离之和为定值
的距离之和为定值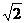 。
。
当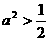 时,点P 到椭圆两个焦点(0,
时,点P 到椭圆两个焦点(0,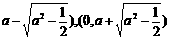 的距离之和为定值2
的距离之和为定值2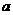 .
.
[模拟试题]
24.(03全国)(本小题满分14分)
 已知常数
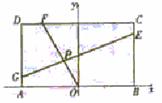
已知常数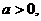 在矩形ABCD中,AB=4,BC=4
在矩形ABCD中,AB=4,BC=4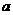 ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且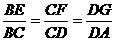 ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
23.(03天津)本小题主要考查函数,不等式等基本知识,考查运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解:由题设可知,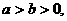 记
记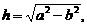 设P的坐标为(0,
设P的坐标为(0,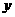 ),则P至三镇距离的平方和为
),则P至三镇距离的平方和为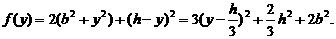 所以,当
所以,当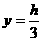 时,函数
时,函数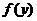 取得最小值. 答:点P的坐标是
取得最小值. 答:点P的坐标是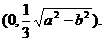
(Ⅱ)解法一:P至三镇的最远距离为 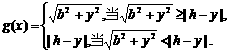
由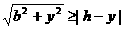 解得
解得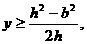 记
记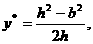 于是
于是
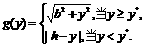 当
当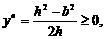 即
即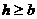 时,
时,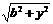 在[
在[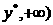 上是增函数,而
上是增函数,而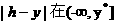 上是减函数. 由此可知,当
上是减函数. 由此可知,当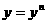 时,函数
时,函数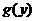 取得最小值. 当
取得最小值. 当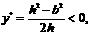 即
即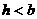 时,函数
时,函数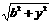 在[
在[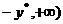 上,当
上,当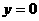 时,取得最小值
时,取得最小值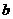 ,而
,而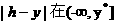 上为减函数,且
上为减函数,且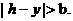 可见, 当
可见, 当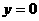 时, 函数
时, 函数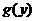 取得最小值. 答当
取得最小值. 答当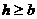 时,点P的坐标为
时,点P的坐标为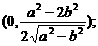 当
当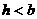 时,点P的坐标为(0,0),其中
时,点P的坐标为(0,0),其中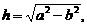
解法二:P至三镇的最远距离为 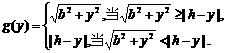 由
由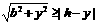 解得
解得
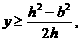 记
记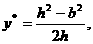 于是
于是
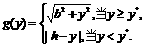
当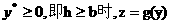 的图象如图
的图象如图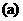 ,因此,当
,因此,当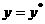 时,函数
时,函数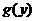 取得最小值.
取得最小值.
 当
当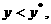 即
即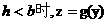 的图象如图
的图象如图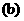 ,因此,当
,因此,当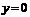 时,函数
时,函数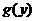 取得最小值.
取得最小值.
答:当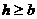 时,点P的坐标为
时,点P的坐标为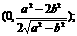 当
当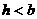 ,点P的坐标为(0,0),其中
,点P的坐标为(0,0),其中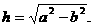
解法三:因为在△ABC中,AB=AC=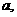 所以△ABC的外心M在射线AO上,其坐标为
所以△ABC的外心M在射线AO上,其坐标为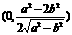 ,
,
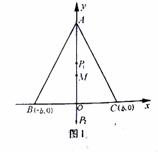 且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,
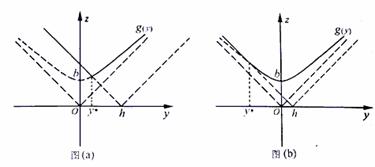
若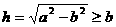 (如图1),则点M在线段AO上,
(如图1),则点M在线段AO上,
这时P到A、B、C三点的最远距离为
P1C和P2A,且P1C≥MC,P2A≥MA,所以点P与外心M
重合时,P到三镇的最远距离最小.
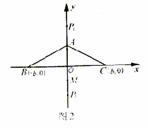 若
若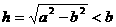 (如图2),则点M在线段AO外,这时
(如图2),则点M在线段AO外,这时
P到A、B、C三点的最远距离为P1C或P2A,
且P1C≥OC,P2A≥OC,所以点P与BC边中点O重合时,
P到三镇的最远距离最小为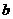 .
.
答:当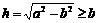 时,点P的位置在△ABC的外心
时,点P的位置在△ABC的外心
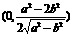 ;当
;当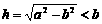 时,点P的位置在原点O.
时,点P的位置在原点O.
22.(03天津)(本小题满分14分)
有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
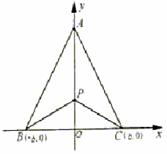 (Ⅰ)若希望点P到三镇距离的平方和为最小,
(Ⅰ)若希望点P到三镇距离的平方和为最小,
点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小,
点P应位于何处?
18.本小主要考查直线与椭圆等基本知识,考查分析问题和解决问题的能力.满分15分.
(Ⅰ)解:椭圆方程为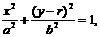 焦点坐标为
焦点坐标为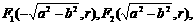
离心率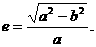
(Ⅱ)证明:将直线CD的方程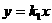 代入椭圆方程,得
代入椭圆方程,得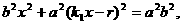
整理得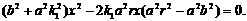 根据韦达定理,得
根据韦达定理,得
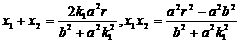 所以
所以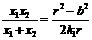 ①
①
将直线GH的方程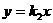 代入椭圆方程,同理可得
代入椭圆方程,同理可得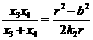 ,
,
 由①,②得
由①,②得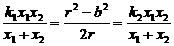 所以结论成立.
所以结论成立.
(Ⅲ)证明:设点P(p,0),点Q(q,0),由C、P、H共线,
得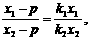 解得
解得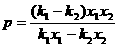 ,
,
由D、Q、G共线,同理可得
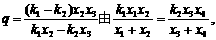
变形得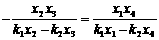
即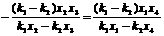
所以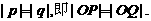
21.(03天津)(本小题满分15分)
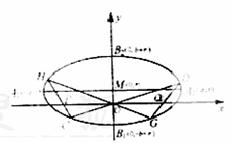
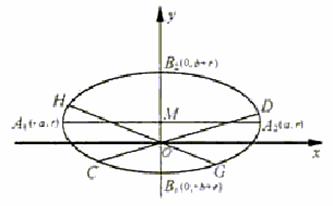
如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(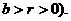
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率;
(Ⅱ)直线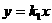 交椭圆于两点
交椭圆于两点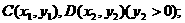 直线
直线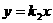 交椭圆于两点
交椭圆于两点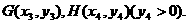 求证:
求证: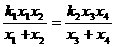 ;
;
(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交x轴于点P,GD交x轴于点Q.
求证:|OP|=|OQ|. (证明过程不考虑CH或GD垂直于x轴的情形)
20.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,满分14分。
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵i=(1,0),c=(0,a), ∴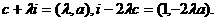
因此,直线OP和AP的方程分别为 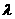 y=ax和y-a=-2
y=ax和y-a=-2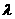 ax .
ax .
消去参数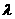 ,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
整理得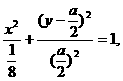 ①
①
因为a>0,所以得:
(i)当a=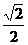 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当0<a<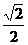 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E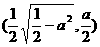 和
和
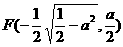 为合乎题意的两个定点;
为合乎题意的两个定点;
(iii)当a>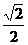 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E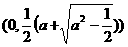 和F
和F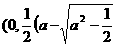 ))为合乎题意的两个定点.
))为合乎题意的两个定点.
19.(03天津)(本小题满分14分)
已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
18.(03广东)(每小题满分14分)
已知常数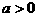 ,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且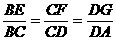 ,P为GE与OF的交点(如图)。问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由。
,P为GE与OF的交点(如图)。问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由。
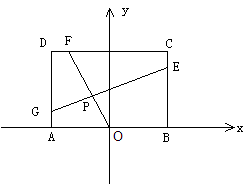
解:根据题设条件,首先求出点P坐标满足的方程,据此再判定是否存在两定点,使得P到两定点距离的和为定值。
按题意有
设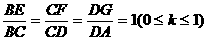
由此有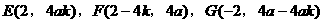
直线OF的方程为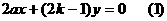
直线CE的方程为: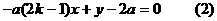
从(1)(2)消去参数k,得点P(x,y)坐标满足方程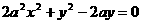
整理得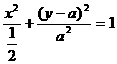
当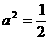 时,点P的轨迹为圆弧,所以不存在符合题意的两点。
时,点P的轨迹为圆弧,所以不存在符合题意的两点。
当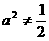 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
当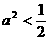 时,点P到椭圆两个焦点
时,点P到椭圆两个焦点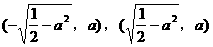 的距离之和为定值
的距离之和为定值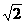
当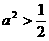 时,点P到椭圆两个焦点
时,点P到椭圆两个焦点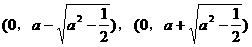 的距离之和为定值2a。
的距离之和为定值2a。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com