
题目列表(包括答案和解析)
5. 抛物线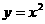 上有A、B、C三点横坐标依次为
上有A、B、C三点横坐标依次为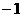 , 2 , 3在
, 2 , 3在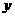 轴一点D纵坐标为6,则四边形ABCD为( )
轴一点D纵坐标为6,则四边形ABCD为( )
A. 正方形 B. 菱形 C. 平行四边形 D. 任意四边形
4. 已知抛物线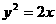 的焦点为F,定点
的焦点为F,定点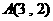 ,在
,在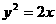 上取动点P,则
上取动点P,则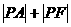 取最小值时,P点坐标为( )
取最小值时,P点坐标为( )
A. 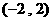 B.
B. 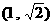 C.
C. 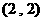 D.
D.
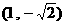
3. 过抛物线的焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影为 ,
,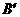 。则
。则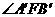
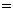 ( )
( )
A. 45° B. 60° C. 75° D. 90°
2. 若抛物线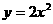 上两点
上两点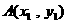
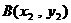 关于直线
关于直线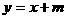 对称,则
对称,则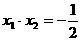 ,则
,则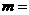 ( )
( )
A. 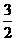 B. 2 C.
B. 2 C.
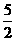 D.
3
D.
3
1. 抛物线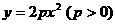 上一点M到位点F的距离为
上一点M到位点F的距离为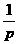 则该点纵坐标为( )
则该点纵坐标为( )
A. 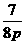 B.
B. 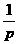 C.
C.
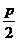 D.
D.
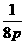
(二)求轨迹方程的注意事项:
1. 求轨迹方程的关键是在纷繁复杂的运动变化中,发现动点P的运动规律,即P点满足的等量关系,因此要学会动中求静,变中求不变。

来表示,若要判断轨迹方程表示何种曲线,则往往需将参数方程化为普通方程。
3. 求出轨迹方程后,应注意检验其是否符合题意,既要检验是否增解,(即以该方程的某些解为坐标的点不在轨迹上),又要检验是否丢解。(即轨迹上的某些点未能用所求的方程表示),出现增解则要舍去,出现丢解,则需补充。检验方法:研究运动中的特殊情形或极端情形。
[典型例题]
例1. 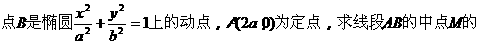
轨迹方程。
分析:题中涉及了三个点A、B、M,其中A为定点,而B、M为动点,且点B的运动是有规律的,显然M的运动是由B的运动而引发的,可见M、B为相关点,故采用相关点法求动点M的轨迹方程。
解:设动点M的坐标为(x,y),而设B点坐标为(x0,y0)
则由M为线段AB中点,可得
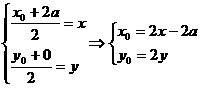
即点B坐标可表为(2x-2a,2y)

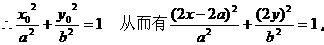

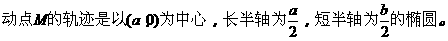
例2. 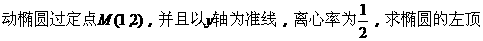
点A的轨迹方程。
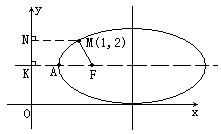
分析:先画出示意图,如图所示:根据已知条件:动椭圆过M(1,2)且以y轴为其准线,可见该椭圆位于y轴右侧,注意到点M在椭圆上,故联想到椭圆的几何性质:椭圆上任一点到焦点的距离与到相应准线的距离之比等于离心率。即可发现间接涉及动顶点A的等量关系。只需用A的坐标先表示出左焦点F的坐标,即可列出轨迹方程。
解:
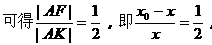
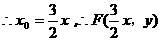
又∵M在椭圆上,
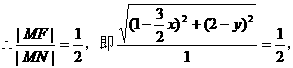
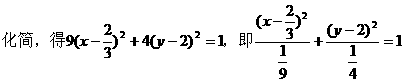
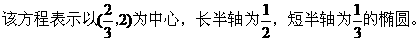
例3. 过点P(2,4)作两条互相垂直的直线l1,l2,若l1交x轴于A点,l2交y轴于B点,求线段AB的中点M的轨迹方程。
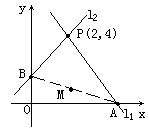
分析1:设M(x,y),由已知l1⊥l2,联想到两直线垂直的充要条件:k1k2=-1,即可列出轨迹方程,关键是如何用M点坐标表示A、B两点坐标。事实上,由M为AB的中点,易找出它们的坐标之间的联系。
解法1:设M(x,y),∵M为AB中点,∴A(2x,0),B(0,2y)。
又l1,l2过点P(2,4),且l1⊥l2
∴PA⊥PB,从而kPA·kPB=-1,
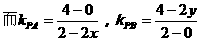
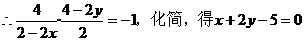
注意到l1⊥x轴时,l2⊥y轴,此时A(2,0),B(0,4)
中点M(1,2),经检验,它也满足方程x+2y-5=0
综上可知,点M的轨迹方程为x+2y-5=0。
分析2:解法1中在利用k1k2=-1时,需注意k1、k2是否存在,故而分情形讨论,能否避开讨论呢?只需利用△PAB为直角三角形的几何特性:
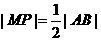
解法2:设M(x,y),连结MP,则A(2x,0),B(0,2y),
∵l1⊥l2,∴△PAB为直角三角形
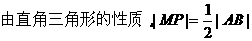
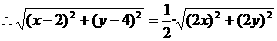
化简,得x+2y-5=0,此即M的轨迹方程。
分析3:从运动的角度观察发现,点M的运动是由直线l1引发的,可设出l1的斜率k作为参数,建立动点M坐标(x,y)满足的参数方程。
解法3:设M(x,y),设直线l1的方程为y-4=k(x-2),(k≠0)

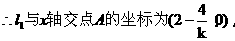

∵M为AB的中点,
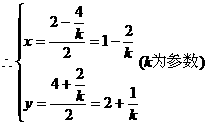
消去k,得x+2y-5=0。
另外,当k=0时,AB中点为M(1,2),满足上述轨迹方程;
当k不存在时,AB中点为M(1,2),也满足上述轨迹方程。
综上所述,M的轨迹方程为x+2y-5=0。
例4. 已知定点A(2,0),点Q是圆x2+y2=1的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程。
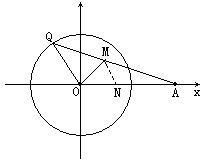
分析1: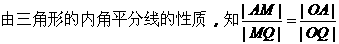
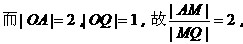

若设出M(x,y),则由分点坐标公式,可表示出点Q的坐标,因Q、M为相关点,(Q点运动导致点M运动),可采用相关点法求点M的轨迹方程。
解法1:设M(x,y),

∵M在AQ上,
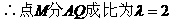 ,
,

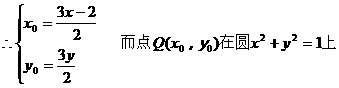
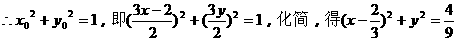

分析2:
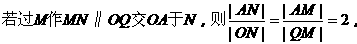
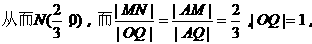


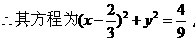
而当∠AOQ=180°时,其角分线为y轴,它与AQ交点为原点O,显然,该点也满足上述轨迹方程。
注:此种解法为定义法。
例5. 如图,给出定点A(a,0),(a>0)与定直线l:x=-1,点B是l上动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值关系。
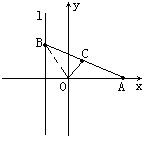
分析:由OC是∠AOB的平分线,可联想到如下结论:
(1)点C到∠AOB的两边OA,OB的距离相等;
(2)OC与OA、OB所成的角相等。
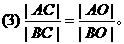
对于(1)、(2)、(3),若再注意到点C在直线AB上,则可求得轨迹方程。因此,本题从不同角度入手,则有不同解法。
解法1:设B(-1,b),C(x,y),直线OB的方程为y=-bx,即bx+y=0,
∵OC平分∠AOB,∴点C到角的两边距离相等。
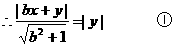
又∵点C在直线AB上,∴A、B、C三点共线
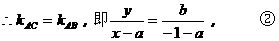
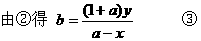
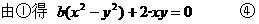
把③代入④,得
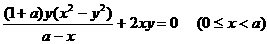
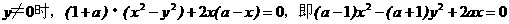
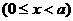
y=0时,b=0,∠AOB=180°,点C坐标为(0,0),满足上述方程。
故方程(a-1)x2-(a+1)y2+2ax=0是点C的轨迹方程。
当a=1时,方程为y2=x,(0≤x<1),它表示抛物线的一段;
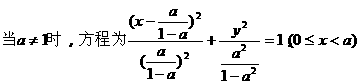
∴0<a<1时,轨迹为椭圆弧;a>1时,轨迹为双曲线弧。
解法2:设B(-1,b),C(x,y)
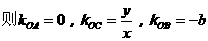
∵OC平分∠AOB ∴∠AOC=∠COB ∴tg∠AOC=tg∠COB,
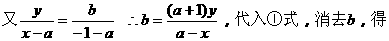
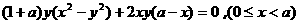
以下略,(见解法1的相应部分)
解法3:设B(-1,b),C(x,y),又A(a,0)
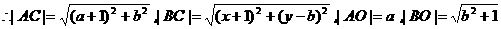
∵OC平分∠AOB,由三角形内角平分线性质,得
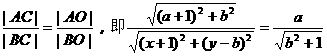
整理,得(b2+1)·[(a+1)2+b2]=a2[(x+1)2+(y-b)2]
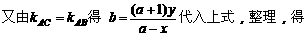
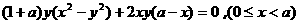
以下略。(同解法1的相应部分)
[模拟试题]
1. 长为3a(a>0)的线段AB的两端点A、B分别在y轴、x轴上运动,P点分线段AB或正比2:1,求点P的轨迹方程。
2. △ABC的顶点B、C 双曲线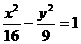 的焦点,点C在抛物线y=4x2上运动,求△ABC的重心G的轨迹方程。
的焦点,点C在抛物线y=4x2上运动,求△ABC的重心G的轨迹方程。
3. 自双曲线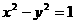 上的动点A引直线x+y=2的垂线,垂足为B,求线段AB中点M的轨迹方程。
上的动点A引直线x+y=2的垂线,垂足为B,求线段AB中点M的轨迹方程。
4. 已知定点A(-1,0),B(2,0),P为动点,且∠PBA=2∠PAB,求动点P的轨迹方程。
5. 以双曲线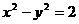 的右准线l为左准线,以双曲线的右焦点F为左焦点的椭圆C的短轴顶点为B,求BF中点M的轨迹方程。
的右准线l为左准线,以双曲线的右焦点F为左焦点的椭圆C的短轴顶点为B,求BF中点M的轨迹方程。
(一)求轨迹方程的一般方法:
1. 待定系数法:如果动点P的运动规律合乎我们已知的某种曲线(如圆、椭圆、双曲线、抛物线)的定义,则可先设出轨迹方程,再根据已知条件,待定方程中的常数,即可得到轨迹方程,也有人将此方法称为定义法。
2. 直译法:如果动点P的运动规律是否合乎我们熟知的某些曲线的定义难以判断,但点P满足的等量关系易于建立,则可以先表示出点P所满足的几何上的等量关系,再用点P的坐标(x,y)表示该等量关系式,即可得到轨迹方程。
3. 参数法:如果采用直译法求轨迹方程难以奏效,则可寻求引发动点P运动的某个几何量t,以此量作为参变数,分别建立P点坐标x,y与该参数t的函数关系x=f(t),y=g(t),进而通过消参化为轨迹的普通方程F(x,y)=0。
4. 代入法(相关点法):如果动点P的运动是由另外某一点P'的运动引发的,而该点的运动规律已知,(该点坐标满足某已知曲线方程),则可以设出P(x,y),用(x,y)表示出相关点P'的坐标,然后把P'的坐标代入已知曲线方程,即可得到动点P的轨迹方程。
专题复习--求轨迹方程
(一)知识与方法要点:
直线与圆锥曲线的关系问题是平面解析几何中的重要问题,一方面它能很好地把有关直线方程的知识和圆锥曲线方程的知识综合起来;另一方面,其中蕴藏了丰富的思想方法,是历年高考试题中的常考常新的内容,从而也就成为高三总复习的着力点
常见的问题有:
1. 直线与圆锥曲线位置关系的研究。
包括位置关系的判定,位置关系与参数值,位置关系与曲线方程等。
2. 直线与圆锥曲线相交成弦的问题。
包括弦长的计算,弦的中点,最值,由弦长或弦的中点的几何性质确定直线方程或圆锥曲线的方程,对称性问题等等。
基本的思想方法:
1. 直线与圆锥曲线的位置关系是由它们的方程组成的方程组的解的情形来确定的,因此要学会利用对方程组的解的情况的讨论来研究直线与圆锥曲线的位置关系。反之亦然,这种思考方法就是解析几何的坐标法。
2. 分析直线与圆锥曲线的位置关系时,要注意对称性的应用和数形结合思想的应用,以及方程、函数的思想、等价转化的思想、分类讨论的思想的运用。
3. 直线l:y=kx+b与圆锥曲线C:F(x,y)=0相交所得弦长的计算方法(公式):
设l与曲线C相交于两点A(x1,y1),B(x2,y2),则
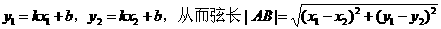
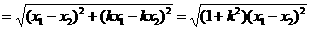
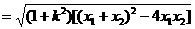
如此以来,便与一元二次方程f(x)=0的根与系数的关系公式建立了联系,自然地,就需联立直线l与曲线C的方程,消元,化出关于x的一元二次方程。(注意,该方程的两个实根恰为A,B两点的横坐标x1,x2)
[典型例题]
例1. 顶点在原点,焦点在x轴上的抛物线被直线l:y=2x+1截得的弦长为
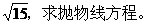
分析:依题意可知抛物线的开口或向左或向右,而标准方程中均有p>0,为了统一起见,不妨设出抛物线方程的统一形式:y2=2mx(m∈R,且m≠0),再根据弦长为
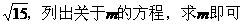
解:设所求抛物线方程为y2=2mx(m∈R且m≠0),另设l与该抛物线交于A(x1,y1),B(x2,y2),
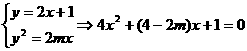
一方面,因l与抛物线相交于两点,故Δ=(4-2m)2-16>0,
解得m<0或m>4
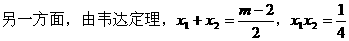
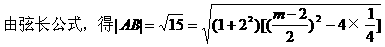
解得m=-2或m=6,显然均满足题意。
故所求抛物线的方程为y2=-4x或y2=12x。
注:本例中体现了方程的思想方法,即为了求抛物线,先设出其方程,然后利用已知条件待定所设的参数m,把问题转化为解关于m的方程。
例2. 设过原点的直线l与抛物线y2=4(x-1)交于A、B两点,且以AB为直径的圆恰好过抛物线的焦点F,
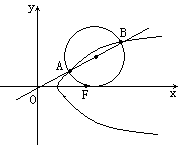
(1)求直线l的方程;
(2)求|AB|的长。
分析:(1)欲求l的方程,只需待定其斜率k,为此就需寻求等量关系,以便列出关于k的方程。由已知条件,发现:AF⊥BF,从而得到等量关系kAF·kBF=-1,从而k可求
(2)一旦直线l确定,则求弦长|AB|迎刃而解。
解:(1)设直线l的方程为y=kx,A(x1,y1),B(x2,y2)
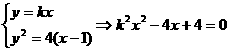
显然k=0时,l与x轴重合,不合题意,故k≠0,从而有
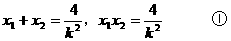
又由已知条件,得AF⊥BF,∴kAF·kBF=-1,又F(2,0)

而y1=kx1,y2=kx2,代入上式,整理,得
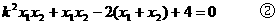
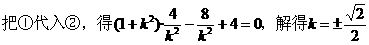

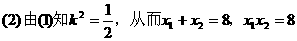
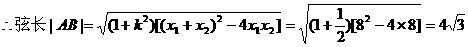
例3. 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,其右焦点到直线
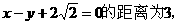
(1)求椭圆方程;
(2)椭圆与直线y=kx+m(k≠0)相交于不同两点M、N,当|AM|=|AN|时,求m的取值范围。
分析:

来待定出a即可。
(2)由椭圆与直线相交于不同两点,可得知由它们的方程联立消元所得的一元二次方程有两个不等实根,从而有Δ=f(m,k)>0;另一方面,又由|AM|=|AN|,可得点A在线段MN的垂直平分线上,设MN中点为P,则有MN⊥AP,从而kMN·kAP=-1,即g(m,k)=0,只需联立f(m,k)>0及g(m,k)=0消去k,解关于m的不等式即可,求得m的取值范围。
解:
而b=1,右焦点设为F(c,0),
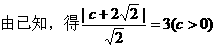
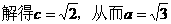

(2)设P为线段MN中点,由|AM|=|AN|得MN⊥AP,
从而kMN·kAP=-1 ①
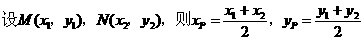
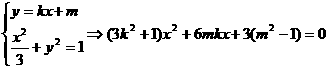
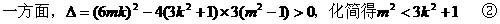
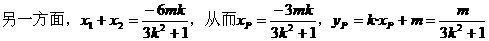
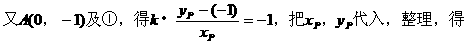
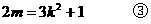
由②③,消去k2,得m2<2m,解得0<m<2。

例4. 直线m:y=kx+1和双曲线x2-y2=1的左支交于A、B两点,直线l过点P(-2,0)和线段AB的中点,求直线l在y轴上的截距b的取值范围。
分析:本题的目标是求参数b的取值范围,与例3中第(2)问,在方法上相同,一方面,由直线m与双曲线左支交于两点,可得关于k、b的不等式,Δ=f(k,b)>0,但应注意A、B两点的横坐标xA,xB均小于0;另一方面,由直线l过P及AB中点,又可得到关于k,b的等量关系g(k,b)=0,联立f(k,b)>0及g(k,b)=0,可求b的取值范围。
解: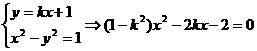
设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),则由题意,得
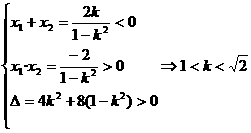
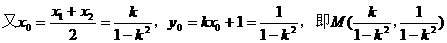
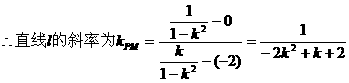
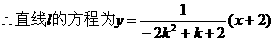

注:求b的取值范围,即求以k为自变量的函数b=f(k)的值域。
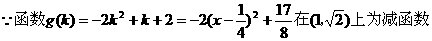
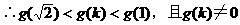
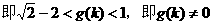
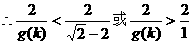
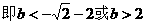
例5. 
交于A,与另一渐近线l2交于点B,求证:线段AB被双曲线的左准线平分。
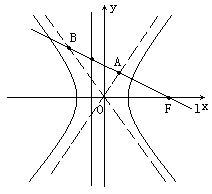
分析:本题的一般思路为:设出l的点斜式方程→分别与l1,l2的方程联立,表出A,B坐标→求出AB中点M的坐标,→验证点M在双曲线的左准线上。事实上,由于

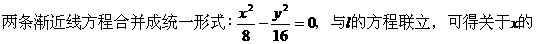
一元二次方程,利用韦达定理,可得xA+xB,进而可求得xM。
解法一:(求A,B交点坐标)
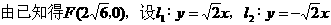
∵l⊥l2
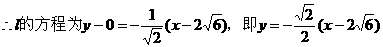
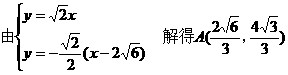
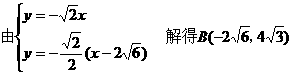


经验证,M在左准线上,故线段AB被双曲线的左准线平分。
解法2: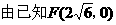
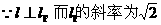

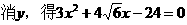



∴AB的中点M在左准线上,即线段AB被双曲线的左准线平分。
例6. 
试求m的取值范围。
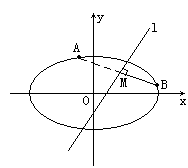
分析:“两点A、B关于直线l对称”,意味着①直线AB与椭圆有两个不同交点;②直线AB⊥l;③线段AB的中点在l上,逐一把这些几何关系化为代数的等式或不等式,即可达到求m的取值范围的目的。
解:设在椭圆上A、B两点关于直线l对称,则依题意,直线AB方程可设为
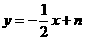

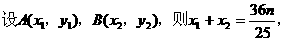
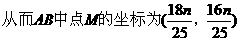
∵点M在l上
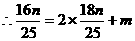
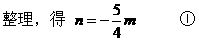
又直线AB与椭圆相交于A、B两点,
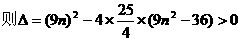
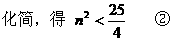
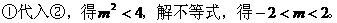
[模拟试题]
1. 设抛物线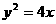 截直线
截直线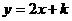 所得弦长为
所得弦长为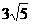 ,
,
(1)求k的值;
(2)以(1)中所得弦长为底边长,以x轴上P点为顶点的三角形的面积为9时,求点P的坐标。
2. 若抛物线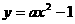 上总存在关于直线l:
上总存在关于直线l: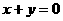 对称的点,求a的取值范围。
对称的点,求a的取值范围。
3. 已知抛物线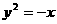 与直线
与直线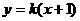 相交于A、B两点,
相交于A、B两点,
(1)求证:OA⊥OB;
(2)当△OAB的面积为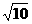 时,求k的值。
时,求k的值。
4. 已知椭圆以坐标轴为对称轴,焦点在x轴上,左焦点到坐标原点、到右焦点、到右准线的距离依次成等差数列,若直线l与椭圆相交于A、B两点,且AB中点M(-2,1),且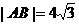 ,求直线l和椭圆的方程。
,求直线l和椭圆的方程。
专题复习--直线与圆锥曲线
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com