
题目列表(包括答案和解析)
2、利用直角坐标系,可以把直角三角形中的三角函数推广到任意角的三角数。三角函数定义是本章重点,从它可以推出一些三角公式。重视用数学定义解题。
设P(x,y)是角α终边上任一点(与原点不重合),记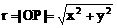 ,则
,则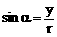 ,
,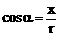 ,
,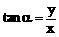 ,
,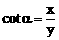 。
。
利用三角函数定义,可以得到(1)诱导公式:即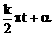 与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。
与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。
1、角的概念的推广。从运动的角度,在旋转方向及旋转圈数上引进负角及大于3600的角。这样一来,在直角坐标系中,当角的终边确定时,其大小不一定(通常把角的始边放在x轴正半轴上,角的顶点与原点重合,下同)。为了把握这些角之间的联系,引进终边相同的角的概念,凡是与终边α相同的角,都可以表示成k·3600+α的形式,特例,终边在x轴上的角集合{α|α=k·1800,k∈Z},终边在y轴上的角集合{α|α=k·1800+900,k∈Z},终边在坐标轴上的角的集合{α|α=k·900,k∈Z}。
在已知三角函数值的大小求角的大小时,通常先确定角的终边位置,然后再确定大小。
弧度制是角的度量的重要表示法,能正确地进行弧度与角度的换算,熟记特殊角的弧度制。在弧度制下,扇形弧长公式=|α|R,扇形面积公式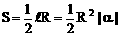 ,其中α为弧所对圆心角的弧度数。
,其中α为弧所对圆心角的弧度数。
3、三角函数的图象及性质。
2、三角公式,包括诱导公式,同角三角函数关系式和差倍半公式等;
1、三角函数的概念及象限角、弧度制等概念;
《三角函数》复习
(三) 解答题
13、设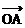 =(3,1),
=(3,1),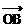 =(-1,2),
=(-1,2),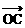 ⊥
⊥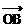 ,
,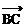 ∥
∥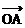 ,试求满足
,试求满足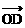 +
+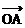 =
=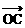 的
的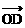 的坐标,其中O为坐标原点。
的坐标,其中O为坐标原点。
14、若 +
+ =(2,-8),
=(2,-8), -
- =(-8,16),求
=(-8,16),求 、
、 及
及 与
与 夹角θ的余弦值。
夹角θ的余弦值。
15、已知| |=
|=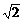 ,|
,| |=3,
|=3, 和
和 夹角为450,求当向量
夹角为450,求当向量 +λ
+λ 与λ
与λ +
+ 夹角为锐角时,λ的取值范围。
夹角为锐角时,λ的取值范围。
(二) 填空题
9、已知{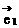 ,
,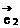 |是平面上一个基底,若
|是平面上一个基底,若 =
=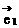 +λ
+λ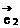 ,
, =-2λ
=-2λ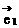 -
-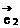 ,若
,若 ,
, 共线,则λ=__________。
共线,则λ=__________。
10、已知| |=
|=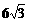 ,|
,| |=1,
|=1, ·
· =-9,则
=-9,则 与
与 的夹角是________。
的夹角是________。
11、设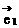 ,
,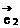 是两个单位向量,它们夹角为600,
是两个单位向量,它们夹角为600,
则(2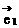 -
-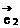 )·(-3
)·(-3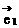 +2
+2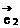 )=____________。
)=____________。
12、把函数y=cosx图象沿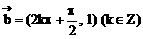 平移,得到函数___________的图象。
平移,得到函数___________的图象。
(一) 选择题
1、平面内三点A(0,-3),B(3,3),C(x,-1),若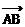 ∥
∥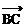 ,则x的值为:
,则x的值为:
A、 -5 B、-1 C、1 D、5
2、平面上A(-2,1),B(1,4),D(4,-3),C点满足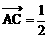
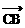 ,连DC并延长至E,使|
,连DC并延长至E,使|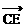 |=
|=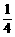 |
|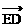 |,则点E坐标为:
|,则点E坐标为:
A、(-8,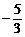 ) B、(
) B、(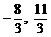 ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,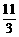 )
)
2、点(2,-1)沿向量 平移到(-2,1),则点(-2,1)沿
平移到(-2,1),则点(-2,1)沿 平移到:
平移到:
3、A、(2,-1) B、(-2,1) C、(6,-3) D、(-6,3)
4、△ABC中,2cosB·sinC=sinA,则此三角形是:
A、 直角三角形 B、等腰三角形 C、等边三角形 D、以上均有可能
5、设 ,
, ,
, 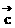 是任意的非零平面向量,且相互不共线,则:
是任意的非零平面向量,且相互不共线,则:
①( ·
· )
)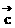 -(
-(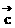 ·
· )
) =0 ②|
=0 ②| |-|
|-| |<|
|<| -
- |
|
③( ·
·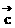 )
) -(
-(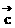 ·
· )
) 不与
不与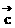 垂直 ④(3
垂直 ④(3 +2
+2 )·(3
)·(3 -2
-2 )=9|
)=9| |2-4
|2-4 |2中,真命题是:
|2中,真命题是:
A、①② B、②③ C、③④ D、②④
6、△ABC中,若a4+b4+c4=2c2(a2+b2),则∠C度数是:
A、600 B、450或1350 C、1200 D、300
7、△OAB中,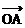 =
= ,
,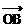 =
= ,
,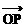 =
=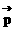 ,若
,若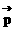 =
=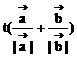 ,t∈R,则点P在
,t∈R,则点P在
A、∠AOB平分线所在直线上 B、线段AB中垂线上
C、AB边所在直线上 D、AB边的中线上
8、正方形PQRS对角线交点为M,坐标原点O不在正方形内部,且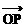 =(0,3),
=(0,3),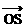 =(4,0),则
=(4,0),则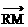 =
=
A、(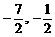 ) B、(
) B、(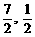 ) C、(7,4) D、(
) C、(7,4) D、(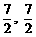 )
)
 例1、如图,
例1、如图,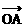 ,
,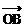 为单位向量,
为单位向量,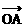 与
与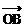 夹角为1200,
夹角为1200, 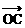 与
与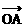 的夹角为450,|
的夹角为450,|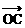 |=5,用
|=5,用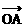 ,
,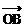 表示
表示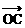 。
。
解题思路分析:
以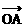 ,
,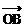 为邻边,
为邻边,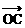 为对角线构造平行四边形
为对角线构造平行四边形
把向量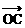 在
在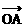 ,
,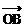 方向上进行分解,如图,设
方向上进行分解,如图,设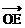 =λ
=λ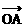 ,
,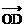 =μ
=μ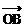 ,λ>0,μ>0
,λ>0,μ>0
则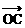 =λ
=λ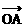 +μ
+μ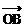
∵ |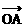 |=|
|=|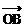 |=1
|=1
∴
λ=|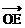 |,μ=|
|,μ=|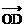 |
|
△OEC中,∠E=600,∠OCE=750,由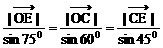 得:
得:
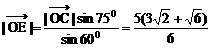
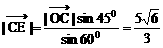
∴
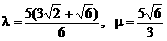
∴
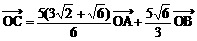
说明:用若干个向量的线性组合表示一个向量,是向量中的基本而又重要的问题,通常通过构造平行四边形来处理
例2、已知△ABC中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求点D和向量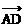 坐标。
坐标。
解题思路分析:
用解方程组思想
设D(x,y),则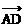 =(x-2,y+1)
=(x-2,y+1)
∵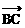 =(-6,-3),
=(-6,-3),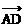 ·
·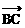 =0
=0
∴ -6(x-2)-3(y+1)=0,即2x+y-3=0 ①
∵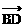 =(x-3,y-2),
=(x-3,y-2),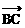 ∥
∥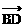
∴ -6(y-2)=-3(x-3),即x-2y+1=0 ②
由①②得: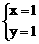
∴ D(1,1),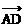 =(-1,2)
=(-1,2)
例3、求与向量 =
=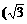 ,-1)和
,-1)和 =(1,
=(1,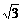 )夹角相等,且模为
)夹角相等,且模为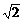 的向量
的向量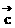 的坐标。
的坐标。
解题思路分析:
用解方程组思想
法一:设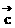 =(x,y),则
=(x,y),则 ·
·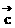 =
=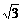 x-y,
x-y, ·
·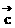 =x+
=x+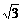 y
y
∵
< ,
,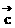 >=<
>=< ,
,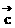 >
>
∴
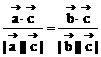
∴
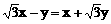
即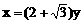 ①
①
又|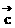 |=
|=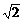
∴ x2+y2=2 ②
由①②得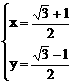 或
或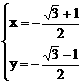 (舍)
(舍)
 ∴
∴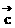 =
=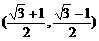
法二:从分析形的特征着手
∵ | |=|
|=| |=2
|=2
 ·
· =0
=0
∴ △AOB为等腰直角三角形,如图
∵ |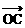 |=
|=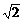 ,∠AOC=∠BOC
,∠AOC=∠BOC
∴ C为AB中点
∴ C(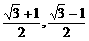 )
)
说明:数形结合是学好向量的重要思想方法,分析图中的几何性质可以简化计算。
例4、在△OAB的边OA、OB上分别取点M、N,使|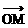 |∶|
|∶|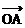 |=1∶3,|
|=1∶3,|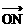 |∶|
|∶|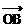 |=1∶4,设线段AN与BM交于点P,记
|=1∶4,设线段AN与BM交于点P,记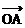 =
=  ,
,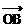 =
= ,用
,用  ,
, 表示向量
表示向量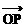 。
。
解题思路分析:
∵ B、P、M共线
∴
记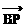 =s
=s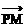
∴
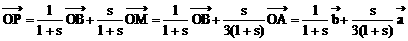 ①
①
同理,记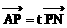
∴
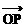 =
=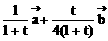 ②
②
∵
 ,
, 不共线
不共线
∴
由①②得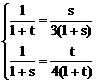 解之得:
解之得: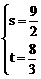
∴
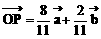
说明:从点共线转化为向量共线,进而引入参数(如s,t)是常用技巧之一。平面向量基本定理是向量重要定理之一,利用该定理唯一性的性质得到关于s,t的方程。
例5、已知长方形ABCD,AB=3,BC=2,E为BC中点,P为AB上一点
(1)利用向量知识判定点P在什么位置时,∠PED=450;
(2)若∠PED=450,求证:P、D、C、E四点共圆。
解题思路分析:
利用坐标系可以确定点P位置
如图,建立平面直角坐标系
则C(2,0),D(2,3),E(1,0)
设P(0,y)
∴
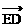 =(1,3),
=(1,3),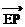 =(-1,y)
=(-1,y)
∴
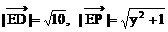
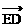 ·
·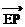 =3y-1
=3y-1
代入cos450=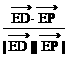
解之得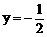 (舍),或y=2
(舍),或y=2
∴ 点P为靠近点A的AB三等分处
(3)当∠PED=450时,由(1)知P(0,2)
∴ 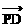 =(2,1),
=(2,1),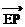 =(-1,2)
=(-1,2)
∴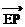 ·
·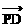 =0
=0
∴ ∠DPE=900
又∠DCE=900
∴ D、P、E、C四点共圆
说明:利用向量处理几何问题一步要骤为:①建立平面直角坐标系;②设点的坐标;③求出有关向量的坐标;④利用向量的运算计算结果;⑤得到结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com