
题目列表(包括答案和解析)
2. 求过圆锥曲线焦点的弦
圆锥曲线的定义都涉及焦点,结合图形运用圆锥曲线的定义,可回避复杂运算。
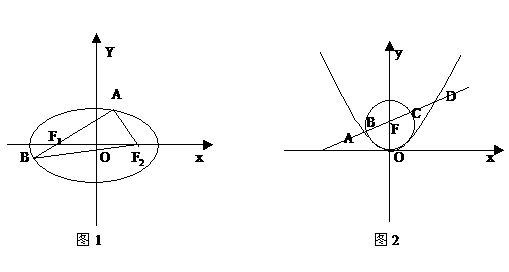
例3 如图1,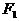 、
、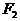 是椭圆
是椭圆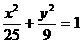 的两个焦点,AB是经过
的两个焦点,AB是经过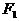 的弦,若
的弦,若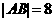 ,则
,则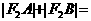 _______________。
_______________。
解:由定义可知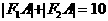 ,
,
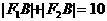 ,
,
则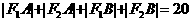 。
。
又由图可知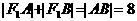 ,
,
因此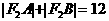 。
。
注:此题如果不结合图形用定义,就很难计算出结果。
1. 求直线与圆的相交弦
因圆比较特殊,故求弦长不采用方法一,可用下面的方法,使运算简单。
设直线方程为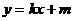 ,圆的方程为
,圆的方程为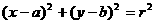 ,圆心为
,圆心为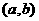 ,直线与圆相交于A、B,圆心到直线的距离为
,直线与圆相交于A、B,圆心到直线的距离为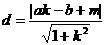 ,则
,则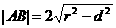 。
。
例2 求圆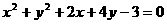 截得直线
截得直线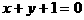 的线段长。
的线段长。
解:由原方程得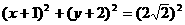 ,圆心为(-1,-2),则
,圆心为(-1,-2),则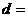
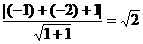 ,从而截得线段长
,从而截得线段长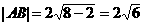 。
。
一般地,求直线与圆锥曲线相交的弦AB长的方法是:
把直线方程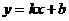 代入圆锥曲线方程中,得到型如
代入圆锥曲线方程中,得到型如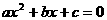 的方程,方程的两根设为
的方程,方程的两根设为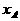 ,
,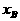 ,判别式为△,则
,判别式为△,则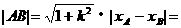
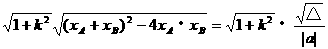 。记住了结果 ,在计算中,直接代
。记住了结果 ,在计算中,直接代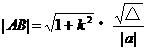 ,就能减少配方、开方等运算过程。
,就能减少配方、开方等运算过程。
例1 求直线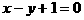 被椭圆
被椭圆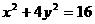 所截得的线段AB的长。
所截得的线段AB的长。
解:把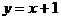 代入椭圆方程
代入椭圆方程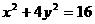 得到
得到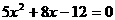 。
。
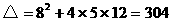 ,
,
则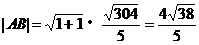 。
。
近几年的高考数学试题,都有运算量大的特点,解析几何部分显得尤为突出,而在解析几何题中,又着重体现在求线段的长。若求线段长的计算方法不当,就会大大增加运算量,直接影响高考成绩。经笔者多年摸索,找到几种计算线段长的简便方法,写出来,供大家参考。
利用曲线系方程可以避免求曲线的交点,因此也可以减少计算。
例7. 求经过两已知圆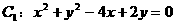 和
和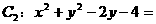 0的交点,且圆心在直线
0的交点,且圆心在直线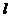 :
: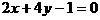 上的圆的方程。
上的圆的方程。
解:设所求圆的方程为:
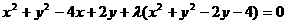
即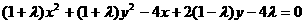 ,
,
其圆心为C(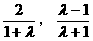 )
)
又C在直线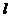 上,
上,
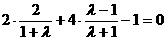 ,解得
,解得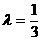 ,代入所设圆的方程得
,代入所设圆的方程得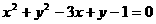 为所求。
为所求。
评注:此题因利用曲线系方程而避免求曲线的交点,故简化了计算。
我们经常设出弦的端点坐标而不求它,而是结合韦达定理求解,这种方法在有关斜率、中点等问题中常常用到。
例5. 已知中心在原点O,焦点在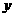 轴上的椭圆与直线
轴上的椭圆与直线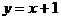 相交于P、Q两点,且
相交于P、Q两点,且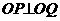 ,
,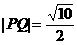 ,求此椭圆方程。
,求此椭圆方程。
解:设椭圆方程为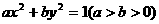 ,直线
,直线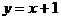 与椭圆相交于P
与椭圆相交于P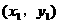 、
、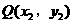 两点。
两点。
由方程组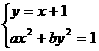 消去
消去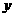 后得
后得
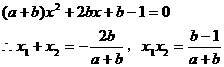
由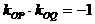 ,得
,得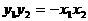 (1)
(1)
又P、Q在直线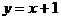 上,
上,
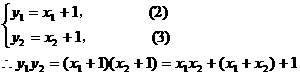
把(1)代入,得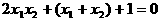 ,
,
即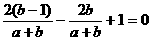
化简后,得
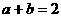 (4)
(4)
由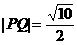 ,得
,得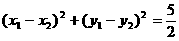
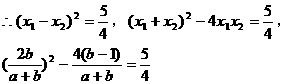
把(2)代入,得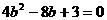 ,解得
,解得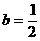 或
或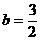
代入(4)后,解得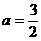 或
或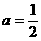
由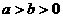 ,得
,得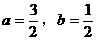 。
。
 所求椭圆方程为
所求椭圆方程为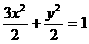
评注:此题充分利用了韦达定理及“设而不求”的策略,简化了计算。
例6. 若双曲线方程为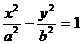 ,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为
,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为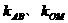 ,则
,则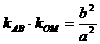
解:设A(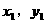 ),B(
),B(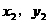 )则M(
)则M(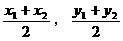 )
)
又 A、B分别在
A、B分别在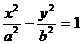 上,则有
上,则有
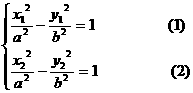
由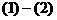 得
得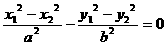 ,
,
即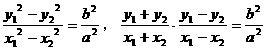 ,
,

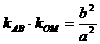
评注:此题充分利用了中点坐标公式斜率公式及“设而不求”的策略,简化了计算。
解析几何的研究对象就是几何图形及其性质,所以在处理解析几何问题时,除了运用代数方程外,充分挖掘几何条件,并结合平面几何知识,这往往能减少计算量。
例1. 已知直线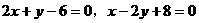 及
及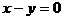 ,求它们所围成的三角形的外接圆方程。
,求它们所围成的三角形的外接圆方程。
解:由直线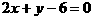 与
与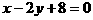 的斜率分别为
的斜率分别为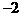 和
和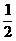 ,得此两条直线互相垂直,即此三角形为直角三角形。
,得此两条直线互相垂直,即此三角形为直角三角形。
由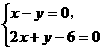 及
及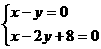 ,可求得直角三角形的斜边所在的两个顶点分别为
,可求得直角三角形的斜边所在的两个顶点分别为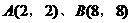 。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为
。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为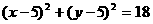
评注:此题若不首先利用三角形是直角三角形这一中间结论,而先求三角形的三个顶点,再解三元一次方程组求圆的一般方程,将会大大增加计算量。
例2. 已知点P(5,0)和圆O: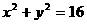 ,过P作直线
,过P作直线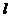 与圆O交于A、B两点,求弦AB中点M的轨迹方程。
与圆O交于A、B两点,求弦AB中点M的轨迹方程。
解: 点M是弦AB中点,
点M是弦AB中点,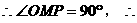 点M是在以OP为直径的圆周上,此圆的圆心为
点M是在以OP为直径的圆周上,此圆的圆心为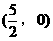 ,半径为
,半径为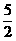 ,所以其方程为
,所以其方程为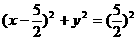 ,即
,即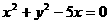 。同时,点M又在圆
。同时,点M又在圆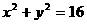 的内部,
的内部,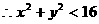 ,即
,即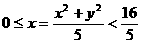 ,所以所求的轨迹方程为
,所以所求的轨迹方程为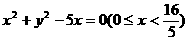
评注:此题若不能挖掘利用几何条件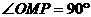 ,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
例3. 求与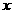 轴相切,圆心在直线
轴相切,圆心在直线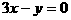 上,且被直线
上,且被直线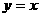 截得的弦长等于
截得的弦长等于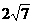 的圆的方程。
的圆的方程。
解:因圆心在直线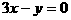 上,故可设圆心
上,故可设圆心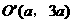
又 圆与
圆与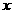 轴相切,
轴相切,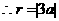 ,
,
 此时可设圆方程为
此时可设圆方程为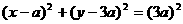
(运用已知条件,找出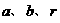 间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
又圆被直线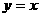 截得的弦长为
截得的弦长为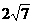 。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用
。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用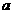 表示出来,便可利用勾股定理求得
表示出来,便可利用勾股定理求得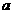 。
。
弦心距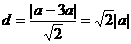

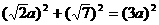 ,解得
,解得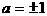
 当
当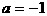 时,
时,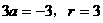 ,圆方程为
,圆方程为
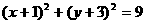
当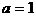 时,
时,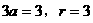 ,圆方程为
,圆方程为
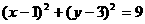
评注:此题若不充分利用圆的半径、半弦、弦心距组成的直角三角形,而用弦长公式,将会增大运算量。
例4. 设直线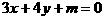 与圆
与圆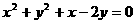 相交于P、Q两点,O为坐标原点,若
相交于P、Q两点,O为坐标原点,若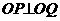 ,求
,求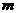 的值。
的值。
解:  圆
圆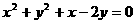 过原点,并且
过原点,并且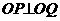 ,
,
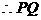 是圆的直径,圆心的坐标为
是圆的直径,圆心的坐标为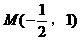
又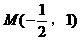 在直线
在直线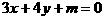 上,
上,
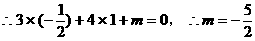 即为所求。
即为所求。
评注:此题若不充分利用一系列几何条件:该圆过原点并且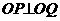 ,PQ是圆的直径,圆心在直线
,PQ是圆的直径,圆心在直线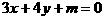 上,而是设
上,而是设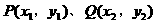 再由
再由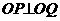 和韦达定理求
和韦达定理求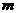 ,将会增大运算量。
,将会增大运算量。
在教学中,学生普遍觉得解析几何问题的计算量较大。事实上,如果我们能够充分利用几何图形、韦达定理、曲线系方程,以及运用“设而不求”的策略,往往能够减少计算量。下面举例说明。
基本知识点:
(1)求解直线与圆锥曲线的位置关系的基本方法是解方程组,进而转化为一元二次方程后利用判别式,应特别注意数形结合的办法。
(2)注意韦达定理的应用。
弦长公式:斜率为k的直线被圆锥曲线截得弦AB,若A、B两点的坐标分别是A(x1,y1),B(x2,y2)则
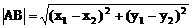
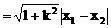
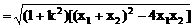
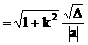
(3)注意斜率不存在的情况的讨论和焦半径公式的使用。
(4)有关中点弦问题
<1>已知直线与圆锥曲线方程,求弦的中点及与中点有关的问题,常用韦达定理。
<2>有关弦的中点轨迹,中点弦所在直线方程,中点坐标问题,有时采用“差分法”可简化运算。
(5)有关圆锥曲线的对称问题
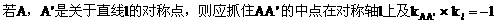
这两个关键条件,同时要记住一些特殊的对称关系,如关于坐标轴对称,关于点对称,关于直线y=±x+b对称。
(6)圆锥曲线中的有关最值问题,常用代数法和几何法解决。
<1>若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决。
<2>若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数,三角函数,均值不等式)求最值。
[例题选讲]
例1. 已知抛物线y2=2px(p>0)。过动点M(a,0)且斜率为l的直线l与该抛物线交于不同的两点A、B
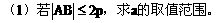
(2)若线段AB的垂直平分线交AB于Q,交x轴于点N,试求三角形MNQ的面积。
解: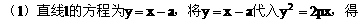
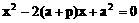
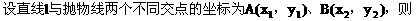
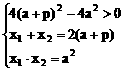
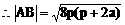
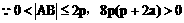
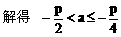
(2)设Q(x3,y3)由中点坐标公式得

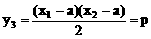
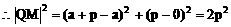
又三角形MNQ为等腰直角三角形
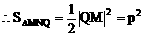
例2. 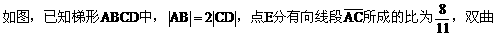 线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
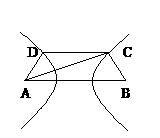
解:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴,因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称。
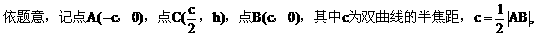
h是梯形的高。
由定比分点坐标公式,得点E的坐标为
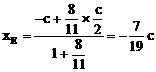
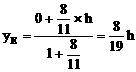

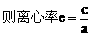
由点C、E在双曲线上,得
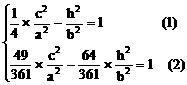
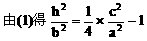
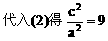
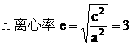
小结:此题涉及解析几何的最根本问题:如何建立坐标系,这也是对学生基本能力的考查,坐标系是一种工具,如果用得好,可以给解题带来方便,但考试时我们不可能对各种情况进行讨论,一般而言,可从对称的角度去考虑。
例3. 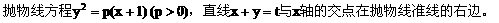
(1)求证:直线与抛物线总有两个不同交点
(2)设直线与抛物线的交点为A、B,且OA⊥OB,求p关于t的函数f(t)的表达式。
 值范围。(1997年·上海高考)
值范围。(1997年·上海高考)
(1)证明:抛物线的准线为
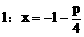
由直线x+y=t与x轴的交点(t,0)在准线右边,得


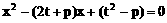
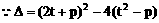
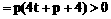
故直线与抛物线总有两个交点。
(2)解:设点A(x1,y1),点B(x2,y2)
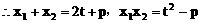
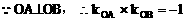
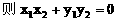
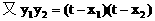
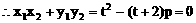
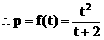
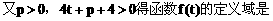
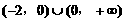
(3)解: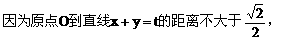
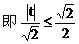
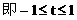
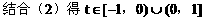
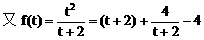
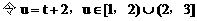
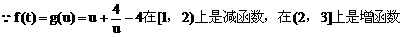
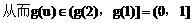
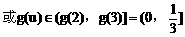
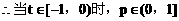
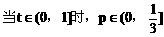
例4. 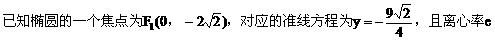
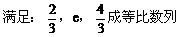
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线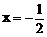 平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
(1)解: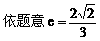
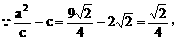
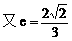
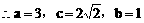
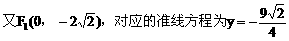


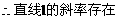
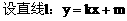
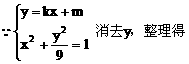

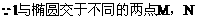
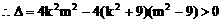
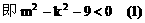
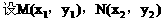
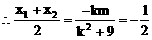
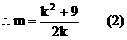
把(2)代入(1)式中得:
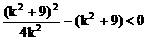
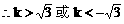
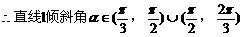
例5. 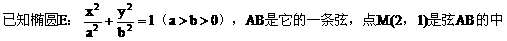 点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
(1)求椭圆E的离心率e;
(2)求双曲线C的方程。
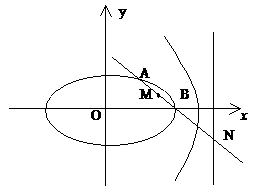
解:(1)因为点M(2,1),点N(4,-1)
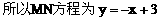
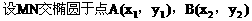
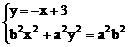
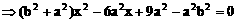
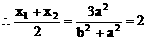
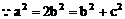
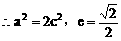

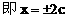
(2)因为ee1=1
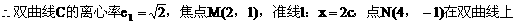
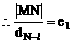
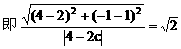
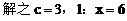
设双曲线C上一点P(x,y)
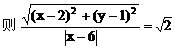
化简得双曲线C的方程:
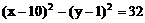
例6. 已知抛物线y2=x上有一条长为l的动弦AB,求AB的中点M到y轴的最短距离。
解:设中点M的坐标为(x,y),利用对称性可设A(x+u,y+v),B(x-u,y-v),依题意有
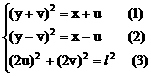
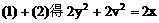
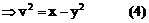
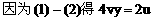
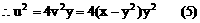
将(4)(5)代入(3)得:
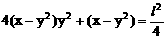
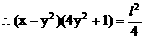
此即M点的方程
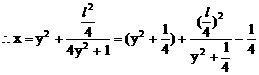
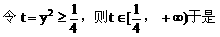
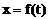
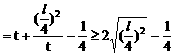
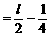
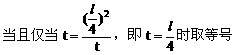


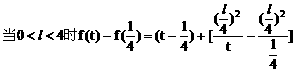
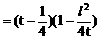
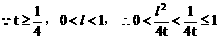
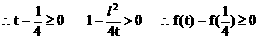

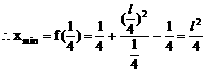
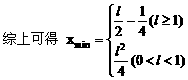
圆锥曲线两焦半径互相垂直问题,常用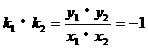 来处理。
来处理。
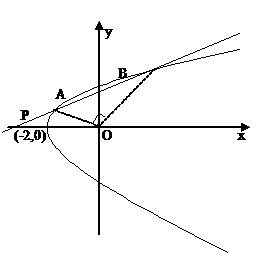
例6 已知直线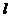 的斜率为
的斜率为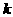 ,且过点
,且过点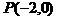 ,抛物线
,抛物线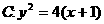 ,直线
,直线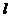 与抛物线C有两个不同的交点(如图)。
与抛物线C有两个不同的交点(如图)。
(1)求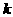 的取值范围;
的取值范围;
(2)直线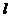 的倾斜角
的倾斜角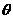 为何值时,A、B与抛物线C的焦点连线互相垂直。
为何值时,A、B与抛物线C的焦点连线互相垂直。
分析:(1)直线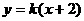 代入抛物线方程得
代入抛物线方程得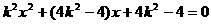 ,
,
由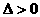 ,得
,得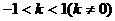 。
。
(2)由上面方程得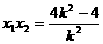 ,
,
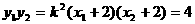 ,焦点为
,焦点为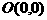 。
。
由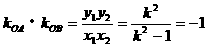 ,得
,得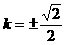 ,
,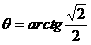 或
或
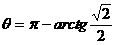 。
。
例7 经过坐标原点的直线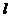 与椭圆
与椭圆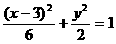 相交于A、B两点,若以AB为直径的圆恰好通过椭圆左焦点F,求直线
相交于A、B两点,若以AB为直径的圆恰好通过椭圆左焦点F,求直线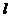 的倾斜角。
的倾斜角。
分析:左焦点F(1,0), 直线y=kx代入椭圆得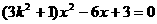 ,
,
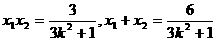 ,
,
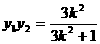 。
。
由AF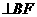 知
知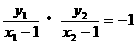 。将上述三式代入得
。将上述三式代入得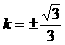 ,
,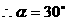 或
或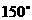 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com