
题目列表(包括答案和解析)
一项是符合题目要求的.
1.满足条件{1,2,3}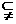 M
M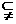 {1,2,3,4,5,6}的集合M的个数是 ( )
{1,2,3,4,5,6}的集合M的个数是 ( )
A.8 B.7 C.6 D.5
20、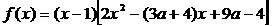 ,在区间
,在区间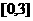 上的最大值与最小值,其中
上的最大值与最小值,其中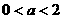 。
。
19、A袋中有1张10元1张5元的钱币,B袋中有2张10元1张5元的钱币,从A袋中任取一张钱币与B袋任取一张钱币互换,这样的互换进行了一次.
求(1)A袋中10元钱币恰是一张的概率;(2)A袋中10元钱币至少是一张的概率.
18、某厂生产某种产品的固定成本(固定投入)为2500元,已知每生产x件这样的产
品需要再增加可变成本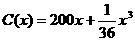 (元),若生产出的产品都能以每件500元
(元),若生产出的产品都能以每件500元
售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
16、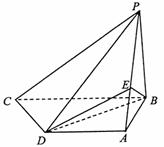 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.
(Ⅰ)求异面直线PA与CD所成的角;
(Ⅱ)求证:PC∥平面EBD;
(Ⅲ)求二面角A-BE-D的大小.
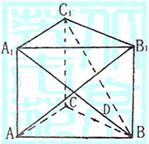 17、正三棱柱ABC-A1B1C1中,D是BC的中点,
17、正三棱柱ABC-A1B1C1中,D是BC的中点,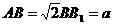 .
.
(1)求异面直线AB1与C1B所成的角;
(2)求点D到平面ACC1的距离;
(3)判断A1B与平面ADC1的位置关系,并证明你的结论.
15、排球比赛的规则是5局3胜制,A、B两队每局比赛获胜的概率分别为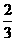 和
和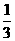 .
.
(Ⅰ)前2局中B队以2:0领先,求最后A、B队各自获胜的概率;
(Ⅱ)B队以3:2获胜的概率.
14、一班级有学生50人,其中男生30人,女生20人。为了了解50名学生与身体状况有关的某项指标,今决定采用分层抽样的方法,抽取一个容量为20的样本,则女生张某被抽中的概率是 。
13、2女3男共5个小孩站成一排,其中2个女孩必须站在两端,则不同的排法共有 种.
12、已知直线m、n及平面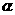 ,其中m∥n,那么在平面
,其中m∥n,那么在平面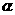 内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.
内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.
其中正确的是 .
11、设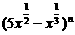 的展开式的各项系数之和为M,且二项式系数之和为N,M-N=992,则展开式中x2项的系数为 .
的展开式的各项系数之和为M,且二项式系数之和为N,M-N=992,则展开式中x2项的系数为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com