
题目列表(包括答案和解析)
1.能够直接利用公式求等差和等比数列的通项;
2.理解等差、等比数列的概念,掌握两种数列的通项公式和前n项和公式,并能运用公式解决一些问题.
[教学目标]
1.理解数列的概念,能用函数的观点认识数列;
4、通过三角问题的分析、求解,提高三角综合运用能力.
[例题讲解]
例题1
(1)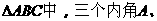 B、C的对边分别是
B、C的对边分别是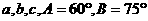 ,
,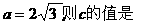 ( )
( )
A 2 B
4 C 2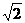 D 不确定
D 不确定
(2)已知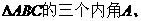 B、C所对的边分别为
B、C所对的边分别为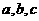 若
若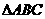 的面积为
的面积为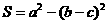 ,则
,则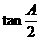 等于 ( )
等于 ( )
A
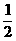 B
B 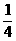 C
C 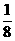 D 1
D 1
(3)若函数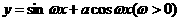 的图象关于点M(
的图象关于点M(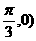 对称,且在x=
对称,且在x=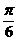 处函数有最小值,则
处函数有最小值,则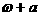 的一个可能的取值为 ( )
的一个可能的取值为 ( )
A 0 B 3 C 6 D 9
(4)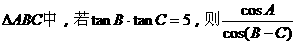 的值为________.
的值为________.
(5)锐角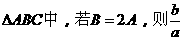 的取值范围是_________.
的取值范围是_________.
(6)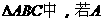 ,B,C成等差数列,则
,B,C成等差数列,则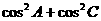 的取值范围是______.
的取值范围是______.
例题2
在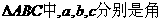 A,B,C的对边,已知
A,B,C的对边,已知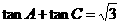
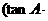
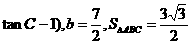 .
.
(1)求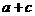 的值; (2)求
的值; (2)求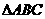 的最大内角.
的最大内角.
例题3
已知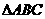 中,角A,B,C的对边为
中,角A,B,C的对边为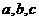 ,向量
,向量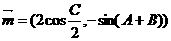 ,
,
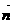 =(
=(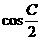 ,2sin(A+B)),
,2sin(A+B)), .
.
(1)求角C; (2)若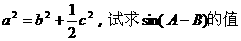 .
.
例题4
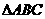 中,三个内角分别是A、B、C,向量
中,三个内角分别是A、B、C,向量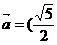
 ),求
),求
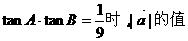 .
.
例题5
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C(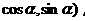
其中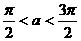 .
.
(1)若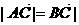 ,求角
,求角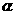 的值;
的值;
(2)若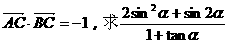 的值.
的值.
3、能以三角为工具,解决三角与向量等有关的问题;
2、会利用正弦定理、余弦定理解三角形;
1、掌握正弦定理、余弦定理及三角形的面积公式;
2、正确运用正弦定理、余弦定理、三角形的面积公式解决三角形中的有关问题.
[教学目标]
1、掌握正弦定理、余弦定理;
2、通过三角函数中“角变换”、“函数名称变换”、“次数变换”等,熟练进行三角式的化简、求值与证明.
[例题讲解]
例题1
(1)已知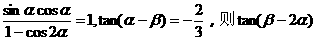 等于 ( )
等于 ( )
A
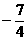 B
B
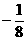 C
C 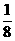 D
D 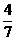
(2)设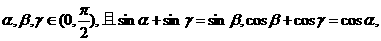 则
则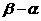 等于
等于
A 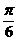 B
B 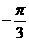 C
C 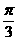 D
D
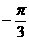 或
或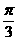 ( )
( )
(3)当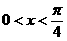 时,函数
时,函数 的最小值是( )
的最小值是( )
A
4 B 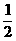 C 2 D
C 2 D 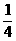
(4)已知 的两根,则
的两根,则 间的关系为
( )
间的关系为
( )
A
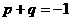 B
B
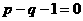 C
C
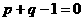 D
D 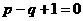
(5)设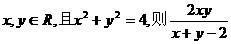 的值域为___________.
的值域为___________.
(6)已知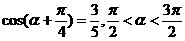 ,则
,则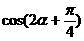 的值为_________.
的值为_________.
例题2
已知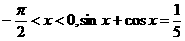
(1)求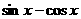 ;
;
(2)求 的值.
的值.
例题3
已知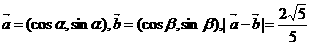 .
.
(1)求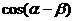 ;
;
(2)若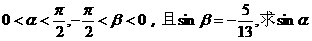 .
.
例题4
已知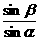 =
=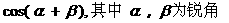 .
.
(1)求证: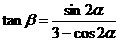 ;
;
(2)求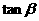 的最大值.
的最大值.
例题5
已知 .
.
高三数学第二轮复习教学案
第三课时:三角综合应用
班级 学号 姓名
[考纲解读]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com