
题目列表(包括答案和解析)
1、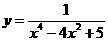 在区间(
在区间(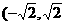 )内的单调性是________
)内的单调性是________
5、函数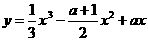 在(1,2)内是减函数,且在(2,+∞)内是增函数,则a=_____。
在(1,2)内是减函数,且在(2,+∞)内是增函数,则a=_____。
例题讲解
例1:已知f(x)=ax3+cx+d(a≠0)是R上奇函数,当x=1时,f(x)取得极值-2。
(1)求f(x)的单调区间和极大值
(2)证明对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立
例2:已知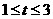 ,
,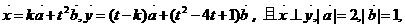
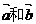 的夹角为600,求k的取值范围。
的夹角为600,求k的取值范围。
例3:一自来水厂的蓄水池中原有水650吨,一天24小时在向水池中注水的同时,蓄水池又向居民供水,若x小时内向居民的总供水量为240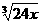 吨,问当每小时向水池注水120吨,一天中何时蓄水池中水量最少。
吨,问当每小时向水池注水120吨,一天中何时蓄水池中水量最少。
课后作业
班级_______学号__________姓名_________
4、函数y=x3-3x2-9x+5在[-4,4]上的最大值为________。
3、已知函数y=f(x)在x=1处的导数为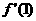 ,若f(1)为函数的极值,则( )
,若f(1)为函数的极值,则( )
A 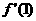 >0 B
>0 B 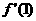 <0 C
<0 C 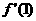 ≠0 D
≠0 D 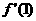 =0
=0
2、若函数f(x)=x3+ax-2在区间(1+∞)内是增函数,则实数a的取值范围( )
A (3,+∞) B [-3,+∞) C (-3,+∞) D(-∞,-3)
1、f(x)=x4-2x2+1的单调增区间为________,单调减区间为________。
2、理解极值、最值的概念,解决实际问题。
基础练习
1、讨论含参数的函数的单调性。
2、掌握运用导数的知识求函数的极值与最值的方法。
重点、难点
1、理解运用导数的知识判断函数的单调性方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com