
题目列表(包括答案和解析)
8.某村计划建造一个室内面积为800m2的矩形蔬菜温室。在温室内,沿左、右两侧与后墙内侧各保留1m宽的通道,沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积为多少?
7.某工厂的产量,第二年比第一年增长的百分率为p1,第三年比第二年增长的百分率为p2,
第四年比第三年增长的百分率为p3,且p1+p2+p3=m,(m为定值),则每年平均增长的百分率的最大值是 ( )
A.1-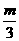 B.
B. 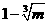 C.
C.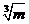 D.
D.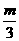
6.设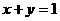 ,
,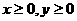 则
则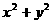 的最大值为_________
的最大值为_________
5.一个人喝150ml啤酒后,血液中的酒精含量上升到0.48mg/ml,在停止喝酒后,血液中的酒精含量每小时减少一半。法律规定:驾驶员血液中的酒精含量不得超过0.08mg/ml,则此人喝酒后至少几小时才能驾驶汽车? ( )
A.2 B. 2.5 C.3 D.3.5
4.某邮局只有面值为0.60元,0.80元,1.10元的三种邮票,现有邮资为7.50元的邮件一件,为使粘贴的邮票张数最少,且邮资恰为7.50元,则至少要购买 张邮票。
3.设点P(x,y)在椭圆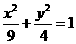 上移动,则x+y的最大值为
。
上移动,则x+y的最大值为
。
2.设一个三角形的三边长为x,y,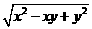 ,则最长边与最短边的夹角等于
。
,则最长边与最短边的夹角等于
。
1.建筑学规定,民用住宅的窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积之比应不小于10%,且这个比值越大,住宅的采光条件越好,问同时增加相等的窗户面积和地板面积,住宅的采光条件是 ( )
A.变好 B. 变坏 C. 不变 D.不确定
9.(选做题) 已知f(x)=lg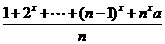 其中a
其中a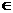 R,n
R,n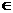 N*。当n
N*。当n 2时,f(x)在(-
2时,f(x)在(- ,1]上有意义,求a的取值范围。
,1]上有意义,求a的取值范围。
高三数学教学案 第六章 不等式
班级 学号 姓名
第十一课时 不等式的综合应用(3)
目标要求
能够利用不等式解决几何中的一些简单问题以及实际应用问题。
例题讲解
例1.将长12cm的铁丝截成两段,用这两段铁丝各自围成一个正三角形,这两个正三角形的面积之和的最小值为 ( )
A.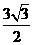 cm2
B.4 cm2
C.
cm2
B.4 cm2
C.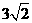 cm2
D.
cm2
D.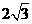 cm2
cm2
例2.将进货单价为80元的商品按90元一个出售时能卖出400个,已知这种商品每个涨价1元,其销售就减少20个,为了赚得最大利润,销售价应定为每个 ( )
A.110 元 B.105元 C.100元 D.95元
例3.已知两点A(3,0),B(0,4),动点P(x,y)在线段AB上运动,则xy的最大值为 ( )
A.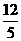 B.
B.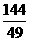 C. 3
D.4
C. 3
D.4
例4.某校把一块边长为2a的等边△ABC的边角地辟为生物园,图中DE把生物园分成面积相等的两部分,D在AB上,E在AC上。
(1)设AD=x,(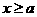 ),ED=y,求用x表示y的函数表达式;
),ED=y,求用x表示y的函数表达式;
(2)如果DE是灌溉水管的位置,为了省钱,希望它最短,DE的位置应该在哪里?如果DE是参观路线希望它最长,DE的位置又应该在哪里? A

 E
E
D
B C
例5.某公司有价值a万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,改造就需要投入,相应就要提高产品的附加值,假设附加值y(万元)与技术改造投入x(万元)之间的关系满足:①y与a-x和x的乘积成正比;②x=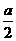 时,y=a2;
时,y=a2;
③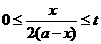 ,其中t为常数且t
,其中t为常数且t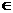 [0,1]。
[0,1]。
(1)设y=f(x),求f(x)的表达式,并写出函数的定义域;
(2)求出产品的附加值y的最大值,并求出此时的技术改造投入的x的值。
例6.甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时。已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为b;固定部分为a元。
(1) 把全程运输成本y(元)表示为速度v (千米/时)的函数,并指出这个函数的定义域;
(2) 为了使全程运输成本最小,汽车应以多大速度行驶?
课后作业
班级 学号 姓名
8.已知数列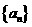 的前n项和为Sn,a1=2,nan+1=Sn+n(n+1)。
的前n项和为Sn,a1=2,nan+1=Sn+n(n+1)。
(1)求数列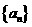 的通项公式;
的通项公式;
(2)设bn=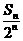 ,如果对一切正整数n都有
,如果对一切正整数n都有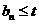 ,求 t的最小值。
,求 t的最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com