
题目列表(包括答案和解析)
2.将 的图象按向量a=
的图象按向量a=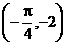 平移,则平移后所得图象的解析式为
平移,则平移后所得图象的解析式为
A.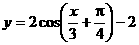 B.
B. 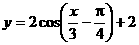
C.  D.
D.
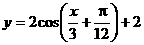
1. 如果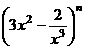 的展开式中含有非零常数项,则正整数n的最小值为
的展开式中含有非零常数项,则正整数n的最小值为
A.3 B.5 C.6 D.10
(17)(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅱ)求B的大小;
(Ⅲ)若a=3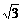 ,c=5,求b.
,c=5,求b.
(18)(本小题满分12分)
某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6.经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.
(19)(本小题满分12分)
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2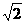 ,SA=SB=
,SA=SB=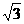 .
.
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.
(20)(本小题满分12分)
设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的x 都有f(x)<c2成立,求c的取值范围.
都有f(x)<c2成立,求c的取值范围.
(21)(本小题满分12分)
设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a1+b3=21,a5+b3=13.
(Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求数列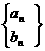 的前n项和Sn.
的前n项和Sn.
(22) (本小题满分12分)
已知椭圆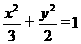 的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为(x0,y0),证明: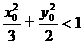 ;
;
(Ⅱ)求四过形ABCD的面积的最小值.
(13)从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g):
492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5-501.5之间的概率约为
(14)函数y=f(x)的图像与函数y=log3x(x>0)的图像关于直线y=x对称,则f(x)=
(15)正四棱锥S-ABCD的底面边长和各测棱长都为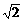 ,点S、A、B、C、D都在同一个球面上,则该球的体积为
,点S、A、B、C、D都在同一个球面上,则该球的体积为
(16)等比数列{an}的前n项和为Sn,已知S1,2S2,3S3成等差数列,则{an}的公比 .
(1)设S=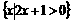 ,T=
,T=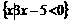 ,则S∩T=
,则S∩T=
(A)Ø
(B)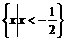
(C)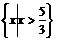 (D)
(D)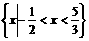
(2)α是第四象限角,cosα= ,则sinα=
,则sinα=
(A)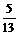 (B)-
(B)- 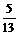 (C)
(C)
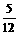 (D)-
(D)-
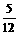
(3)已知向量a=(-5,6),b=(6,5),则a与b
(A)垂直 (B)不垂直也不平行
(C)平行且同向 (D)平行且反向
(4)已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为
(A)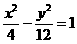 (B)
(B)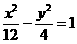
(C)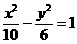 (C)
(C)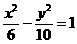
(5)甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有
(A)36种 (B)48种 (C)96种 (D)192种
(6)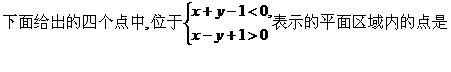
(A)(0,2) (B)(-2,0) (C)(0,-2) (D)(2,0)
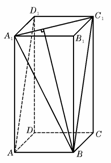 (7)如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为
(7)如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为
(A)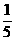
(B)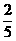
(C)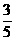
(D)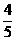
(8)设a>1,函数f(x)=log,x在区间[a,2a]上的最大值与最小值之差为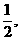 则a=
则a=
(A)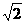 (B)2
(C)2
(B)2
(C)2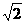 (D)4
(D)4
(9)f(x),g(x)是定义在R上的函数,h(x)=f(x)+ g(x),则“f(x),g(x)均为偶函数”,是“h(x)为偶数”的
(A)充分条件 (B)充分而不必要的条件
(C)必要而不充分的条件 (D)既不充分也不必要的条件
(10)函数y=2cos2x的一个单调增区间是
(A)(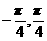 ) (B)(
) (B)(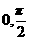 ) (C)(
) (C)(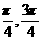 ) (D)(
) (D)(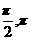 )
)
(11)曲线y=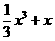 在点(1,
在点(1,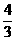 )处的切线与坐标轴围成的三角形面积为
)处的切线与坐标轴围成的三角形面积为
(A)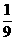 (B)
(B) 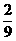 (C)
(C)
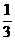 (D)
(D)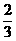
(12)抛物线y2=4x的焦点为F,准线为l,经过F且斜率为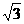 的直线与抛物线在x轴上方的部分相交于点A,AK⊥l,满足为K,则△AKF的面积是
的直线与抛物线在x轴上方的部分相交于点A,AK⊥l,满足为K,则△AKF的面积是
(A)4
(B)3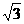 (C)
4
(C)
4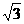 (D)8
(D)8
2007年普通高等学校招生全国统一考试
文科数学
21.(本小题满分14分)
已知函数f(x)=x2+x-1,α、β是方程f(x)=0的两个根(α>β).f′(x)是f(x)的导数.设a1=1,an+1=an-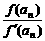 (n=1,2,…).
(n=1,2,…).
(1)求α、β的值;
(2)证明:任意的正整数n,都有an>a;
(3)记bn- (n=1,2,…),求数列{bn}的前n项和Sn.
(n=1,2,…),求数列{bn}的前n项和Sn.
20.(本小题满分14分)
已知a是实数,函数f(x)=2ax2+2x-3-a,如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.
19.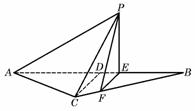 (本小题满分14分)
(本小题满分14分)
如图6所示,等腰△ABC的底边AB=6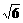 ,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
BE=x,V(x)表示四棱锥P-ACFE的体积.
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
18.(本小题满分14分)
在平面直角坐标系xOy中,已知圆心在第二象限,半径为2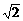 的圆C与直线y=x相切于坐标原点O.椭圆
的圆C与直线y=x相切于坐标原点O.椭圆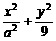 =1与圆C的一个交点到椭圆两点的距离之和为10.
=1与圆C的一个交点到椭圆两点的距离之和为10.
(1)求圆C的方程.
(2)试探安C上是否存在异于原点的点Q,使Q到椭圆右焦点P的距离等于线段OF的长.若存在,请求出点Q的坐标;若不存在,请说明理由.
17.(本题满分12分)
下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=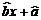 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com