
题目列表(包括答案和解析)
2、函数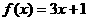 ,若
,若 成立的充分条件是
成立的充分条件是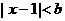 (
(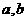 ≥0)画出满足关系的点
≥0)画出满足关系的点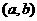 在直角坐标系中表示的区域.
在直角坐标系中表示的区域.
1、点(3,1)和(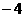 ,6)在直线
,6)在直线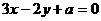 的两侧,则
的两侧,则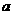 的取值范围是__________.
的取值范围是__________.
4、已知集合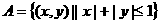 ,集合
,集合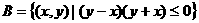 ,
,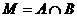 ,则
,则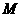 的面积是_________.
的面积是_________.
例题讲解
例1、某工厂制造甲、乙两种产品,已知制造甲产品1kg要用煤9吨,用电力4kw,劳力(按工作日计算)3个;制造乙产品1kg要用煤4吨,电力5kw,劳力10个,又知制成甲产品1kg可获利7万元,制成乙产品1kg可获利12万元,现在工厂只有煤360吨,电力200kw,劳力300个,在这种条件下应生产甲、乙两种产品各多少千克,才能获得最大经济效益?
例2、某人承揽一项业务,需做文字标牌4个,绘画标牌6个,现有两种规格原料,甲种规格每张3㎡,可做文字标牌1个,绘画标牌2个;乙种规格每张2㎡,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?
例3、某工厂加工零件,要在长度为400cm的圆钢上截取长度为61cm和51cm的甲、乙两种规格的圆钢,怎样截取才能使余料为最少?
课后作业
班级_______学号__________姓名_________
3、已知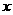 、
、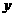 满足
满足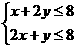 ,目标函数
,目标函数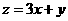 ,当
,当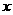 =_________,y=________时,
=_________,y=________时,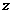 最大值为_________,若又
最大值为_________,若又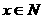 且
且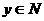 ,则
,则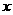 =_________,y=__________时,
=_________,y=__________时,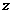 最大值为________.
最大值为________.
2、可以表示图中阴影部分平面区域的二元一次不等式组是_________________.
1、点(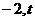 )在直线
)在直线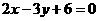 的上方,则实数
的上方,则实数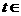 ___________.
___________.
2、线性规划(线性约束条件、可行域、目标函数、最优解)
重点、难点
掌握用线性规划的方法解决一些简单实际问题的步骤:
(1)列表、转化为线性规划问题;(2)设出相关变量建立线性约束条件、目标函数;
(3)画出可行域; (4)找出最优解; (5)回答实际问题
基础练习
1、二元一次不等式表示平面区域;
2、了解线性规划的意义,并会简单应用,提高解决实际问题的能力.
知识概要
1、了解用二元一次不等式(组)表示平面区域;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com