
题目列表(包括答案和解析)
22、(本题满分16分,第1小题8分,第2小题8分)
设函数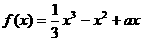 ,
,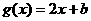 ,当
,当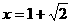 时,
时,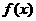 取得极值。
取得极值。
(1)
求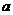 的值,并判断
的值,并判断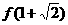 是函数
是函数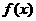 的极大值还是极小值;
的极大值还是极小值;
(2)
当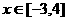 时,函数
时,函数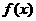 与
与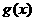 的图象有两个公共点,求
的图象有两个公共点,求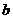 的取值范围。
的取值范围。
21、(本题满分14分,第1小题5分,第2小题9分)
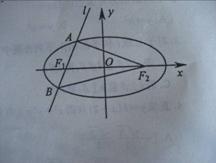 如图,椭圆
如图,椭圆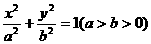 的左、右焦点为
的左、右焦点为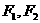 ,过
,过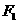 的直线
的直线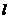 与椭圆相交于
与椭圆相交于 、
、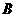 两点。
两点。
(1)
若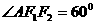 ,且
,且 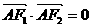 求椭圆的离心率。
求椭圆的离心率。
(2)
若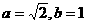 ,求
,求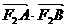 的最大值和最小值。
的最大值和最小值。
20、(本题满分14分,第1小题4分,第2小题5分,第3小题5分)
已知各项均为正数的数列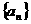 中,
中,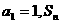 是数列
是数列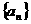 的前
的前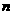 项和,对任意
项和,对任意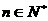 ,有
,有
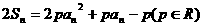
(1)
求常数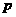 的值;
的值;
(2)
求数列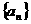 的通项公式;
的通项公式;
(3)
记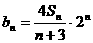 ,求数列
,求数列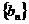 的前
的前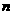 项和
项和 。
。
19、 (本题满分12分,第1小题3分,第2小题4分,第3小题5分)
(本题满分12分,第1小题3分,第2小题4分,第3小题5分)
如图,在四棱锥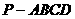 中,ABCD是矩形,
中,ABCD是矩形, ,
,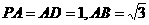 ,
,
点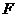 是
是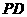 的中点,点
的中点,点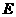 在
在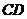 上移动。
上移动。
(1)
求三棱锥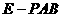 体积;
体积;
(2)
当点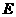 为
为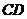 的中点时,试判断
的中点时,试判断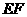 与平面
与平面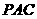 的关系,并说明理由;
的关系,并说明理由;
(3)
求证: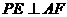
18、(本题满分12分)
要建一间地面面积为20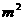 ,墙高为
,墙高为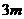 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元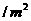 ,其余三面的造价为200元
,其余三面的造价为200元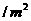 ,屋顶的造价为250元
,屋顶的造价为250元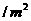 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
17、(本题满分12分,第1小题8分,第2小题4分)
已知函数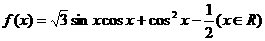
(1)
求函数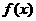 的周期;
的周期;
(2)
函数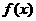 的图象可由函数
的图象可由函数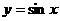 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
16、设函数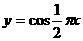 的图象位于
的图象位于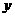 轴右侧所有的对称中心从左依次为
轴右侧所有的对称中心从左依次为 ,则
,则
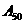 的坐标是
。
的坐标是
。
15、设直线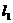 的方程为
的方程为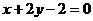 ,将直线
,将直线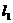 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转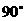 得到直线
得到直线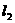 ,则
,则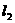 的方程是
。
的方程是
。
14、已知实数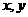 满足约束条件
满足约束条件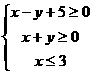 则
则 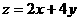 的最小值为
。
的最小值为
。
13、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位: ),可得这个几何体的表面积是
。
),可得这个几何体的表面积是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com