
题目列表(包括答案和解析)
6.两个事件对立是这两个事件互斥的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分且不必要条件
5.某单位有三个科室,为实现减员增效,每科室抽调2人去参加再就业培训,培训后这6人中有2人返回单位,但不回到原科室工作,且每科室至多安排一人,问共有多少种不同的安排方法( )
A.75种 B.42种 C.30种 D.15种
4.设集合M={a|a∈N,1≤a≤10},A是M的三元素子集且至少有两个偶数元素,则这样的集合A的个数是( )
?A.60 B.100 C.120 D.160
3.停车场划出一排12个停车位置,今有8辆车需要停放,要求空车位连在一起,不同的停车方法有( )
A.A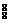 种
B.A
种
B.A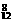 种
C.A
种
C.A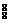 ·C
·C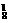 种 D.A
种 D.A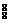 ·C
·C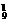 种
种
2.从不同号码的5双鞋中任取4只,其中恰好有一双的取法种数为( )
A.120 B.240 C.180 D.60
1. 8本不同的书分给甲、乙、丙3人,其中有两人各得3本,一人得2本,则不同的分法共有( )
A.560种 B.280种 ?C.1 680种 D.3 360种
16. (本小题满分12分)
已知函数f(x)的定义域为[0,1],且同时满足:
①对任意x∈[0,1],总有f(x)≥2;②f(1)=3;③若x1≥0,x2≥0且x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-2.
(1)求f(0)的值;
(2)试求f(x)的最大值;
(3)设数列{an}的前n项和为Sn,且满足a1=1,Sn= -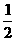 (an-3),n∈N*.
(an-3),n∈N*.
求证:f(a1)+f(a2)+…+f(an)≤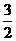 +2n-
+2n-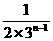 .
.
15. (本小题满分12分)
设等差数列{an}的首项为a(a≠0),公差为2a,前n项和为Sn.记A={(x,y)|x=n,y=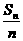 ,n∈N*},B={(x,y)|(x-2)2+y2=1,x、y∈R}.
,n∈N*},B={(x,y)|(x-2)2+y2=1,x、y∈R}.
 (1)若A∩B≠ ?,求a的取值集合;
(1)若A∩B≠ ?,求a的取值集合;
(2)设点P∈A,点Q∈B,当a=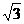 时,求|PQ|的最小值.
时,求|PQ|的最小值.
14. (本小题满分12分)
为了保护三峡库区的生态环境,凡是坡度在25°以上的坡荒地都要绿化造林,经初步统计,在三峡库区坡度大于25°的坡荒地面积约为2640万亩,若从2003年初开始绿化造林,第一年造林120万亩,以后每一年都比前一年多绿化60万亩.
(1)若所有应被绿化造林的坡荒地全部绿化成功,问到哪一年底可使库区的坡荒地全部绿化?
(2)若每万亩绿化造林所植树苗的木材量平均为0.1万立方米,每年树木木材量的自然增长率为20%,那么当整个库区25°以上荒地全部绿化完的哪一年底,一共有木材多少万立方米?(保留1位小数,1.29=5.16,1.28=4.30)
13. (本小题满分12分)
已知等差数列{an}中,a2=8,前10项的和S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺序排列成一个新的
数列{bn},试求新数列{bn}的前n项和An.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com