
题目列表(包括答案和解析)
17.(丁中)方程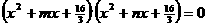 的四个实数根组成一个首项为
的四个实数根组成一个首项为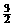 的等比数列,则
的等比数列,则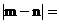
正解: 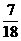 .
.
错因:设方程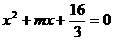 的解为
的解为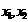 ;方程
;方程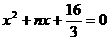 的解为
的解为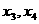 ,则
,则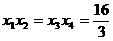 ,不能依据等比数列的性质准确搞清
,不能依据等比数列的性质准确搞清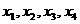 的排列顺序.
的排列顺序.
16.(丁中)设等差数列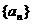 中,
中,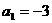 ,且从第5项开始是正数,则公差的范围是
,且从第5项开始是正数,则公差的范围是
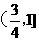
错解: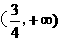
错因:忽视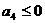 ,即第4项可为0。
,即第4项可为0。
正解: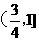
15.(丁中)已知数列{an}的前n项和Sn=an-1(a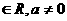 ),则数列{an}_______________
),则数列{an}_______________
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列或者是等比数列 D.既非等差数列又非等比数列
错解:B
错因:通项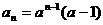 中忽视
中忽视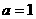 的情况。
的情况。
正解:C
14.(江安中学)有四个命题:
1)
一个等差数列{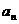 }中,若存在
}中,若存在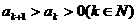 ,则对于任意自然数
,则对于任意自然数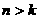 ,都有
,都有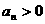 ;
;
2)
一个等比数列{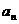 }中,若存在
}中,若存在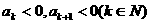 ,则对于任意
,则对于任意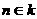 ,都有
,都有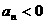 ;
;
3)
一个等差数列{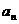 }中,若存在
}中,若存在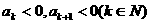 ,则对于任意
,则对于任意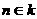 ,都有
,都有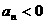 ;
;
4)
一个等比数列{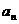 }中,若存在自然数
}中,若存在自然数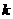 ,使
,使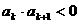 ,则对于任意
,则对于任意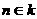 ,都有
,都有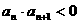 ,其中正确命题的序号是_____。
,其中正确命题的序号是_____。
正解:由等差数列和等比数列的性质得①②④。
误解:“对于等比数列,若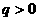 ,各项同号(同正或同负),若
,各项同号(同正或同负),若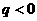 ,各项正,负相间”,学生对此性质把握不清,故认为②④错。
,各项正,负相间”,学生对此性质把握不清,故认为②④错。
13.(江安中学)关于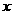 的方程
的方程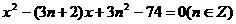 的所有实根之和为_____。
的所有实根之和为_____。
正解:168
 方程有实根,
方程有实根,

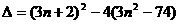 ≥0
≥0
解得: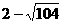 ≤n≤
≤n≤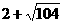
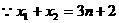
 所有实根之和为
所有实根之和为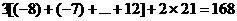
误解:没能根据条件具体确定n的取值,只得出一个关于n的多项式结果。
12.(江安中学)关于数列有下列四个判断:
1)
若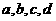 成等比数列,则
成等比数列,则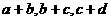 也成等比数列;
也成等比数列;
2)
若数列{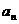 }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{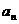 }为常数列;
}为常数列;
3)
数列{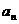 }的前n项和为
}的前n项和为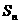 ,且
,且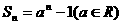 ,则{
,则{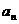 }为等差或等比数列;
}为等差或等比数列;
4)
数列{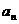 }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{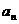 }中不会有
}中不会有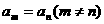 ,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
正解:(2)(4).
误解:(1)(3)。对于(1)a、b、c、d成等比数列。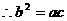
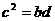
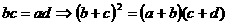
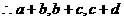 也成等比数列,这时误解。因为特列:
也成等比数列,这时误解。因为特列: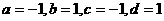 时,
时,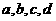 成等比数列,但
成等比数列,但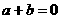 ,
,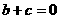 ,
,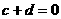 ,即
,即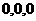 不成等比。
不成等比。
对于(3)可证当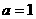 时,为等差数列,
时,为等差数列,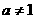 时为等比数列。
时为等比数列。
 时既不是等差也不是等比数列,故(3)是错的。
时既不是等差也不是等比数列,故(3)是错的。
11.(蒲中)已知{an}为递增数列,且对于任意正整数n,an=-n2+λn恒成立,则λ的取值范围是____________
答案:λ>3
点评:利用二次函数单调性讨论较繁,且易错,利用an+1>an恒成立较方便。
10.(蒲中)数列{an}的前n项和Sn=n2+1,则an=____________
答案:an=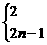
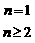
点评:误填2n-1,忽略“an=Sn-Sn-1”成立的条件:“n≥2”。
9.(城西中学)给定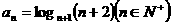 ,定义使
,定义使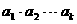 为整数的
为整数的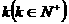 叫做“企盼数”,则在区间(1,62)内的所有企盼数的和是___________.
叫做“企盼数”,则在区间(1,62)内的所有企盼数的和是___________.
正确答案:52
错因:大部分学生难以读懂题意,也就难以建立解题数学模型。
8.(如中)一种产品的年产量第一年为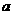 件,第二年比第一年增长
件,第二年比第一年增长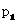 ﹪,第三年比第二年增长
﹪,第三年比第二年增长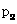 ﹪,且
﹪,且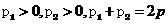 ,若年平均增长
,若年平均增长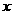 ﹪,则有
﹪,则有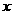 ___
___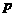 (填
(填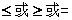 )
)
[错解]
[错解分析]实际问题的处理较生疏,基本不等式的使用不娴熟
[正解]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com