
题目列表(包括答案和解析)
21、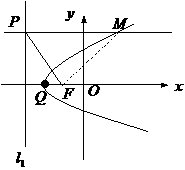 (1)由
(1)由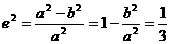 ,得
,得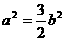
∵直线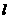 :y=x+2与圆x2+y2=b2相切,∴
:y=x+2与圆x2+y2=b2相切,∴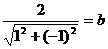 ,解得
,解得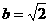 ,则a2=3。
,则a2=3。
故所求椭圆C1的方程为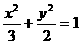 。
。
(2)椭圆C1的左焦点为F(-1,0),左准线为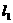 :x=-3。
:x=-3。
如图,连结MF,则|MF|=|MP|,∴点M的轨迹C2是以F为焦点,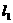 为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设
为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设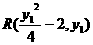 、
、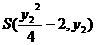 ,由QR⊥RS得
,由QR⊥RS得
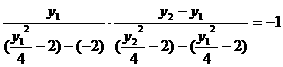
化简得y2=-(y1+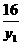 )
)
∴y22=y12+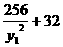 ≥2×16+32=64
≥2×16+32=64
∵|QS|2=[(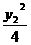 -2)+2]2+y22=
-2)+2]2+y22=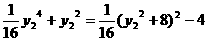
∴当y22=64时,|QS|min=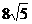 .
.
故|QS|的取值范围是[8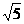 ,+∞)。
,+∞)。
20、 (1)函数y=f(t)的定义域为[0,+∞);值域为{y|y=2n,n∈N*}
 (2)
(2)
(3)y=
19、(1) ∵PA⊥底面ABC,∴PA⊥BE
又∵△ABC是正三角形,且E为AC的中点,∴BE⊥CA
又PA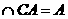 ,∴BE⊥平面PAC
,∴BE⊥平面PAC
∵BE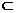 平面PBE,∴平面PBE⊥平面PAC。
平面PBE,∴平面PBE⊥平面PAC。
(2)取CD的中点F,则点F即为所求。
∵E、F分别为CA、CD的中点,∴EF//AD
又EF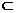 平面PEF,AD
平面PEF,AD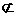 平面PEF,∴AD//平面PEF。
平面PEF,∴AD//平面PEF。
(3)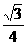
18、(1)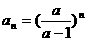 (2)
(2)
17、①当m≠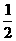 时,A、B、C三点能构成三角形;
时,A、B、C三点能构成三角形;
②当m=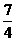 时,三角形ABC为直角三角形,且∠A=90°。
时,三角形ABC为直角三角形,且∠A=90°。
13、(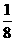 ,0) 14、
,0) 14、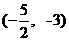 15、10
16、1
15、10
16、1
1、A 2、D 3、A 4、A 5、C 6、A 7、B 8、C 9、A 10、C 11、B 12、C
22、设函数f(x)=sin2x+2a·cosx+a3-a(0≤x≤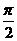 )
)
(1)求f(x)的最大值M(a)。
(2)当a∈[-1,1]时,求函数M(a)的最值。
[答案]
21、已知椭圆C: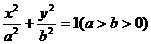 ,它的离心率为
,它的离心率为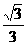 ,直线
,直线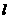 :y=x+2,它与以原点为圆心,以C1的短半轴长为半径的圆相切。
:y=x+2,它与以原点为圆心,以C1的短半轴长为半径的圆相切。
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F,左准线为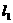 。动直线
。动直线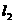 垂直于
垂直于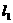 ,垂足为P,线段PF的垂直平分线交
,垂足为P,线段PF的垂直平分线交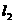 交于点M。点M的轨迹C2与x轴交于点Q,若R、S两点在C2上,且满足QR⊥RS,求|QS|的取值范围。
交于点M。点M的轨迹C2与x轴交于点Q,若R、S两点在C2上,且满足QR⊥RS,求|QS|的取值范围。
20、某种细菌两小时分裂一次,(每一个细菌分裂成两个,分裂所需的时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t)
(1)写出函数y=f(t)的定义域和值域;
(2)在所给坐标系中画出y=f(t);(0≤t<6)的图象;
 (3)写出研究进行到n小时(n≤0,n∈Z)时细菌的总数有多少个(用关于n的式子表示)。
(3)写出研究进行到n小时(n≤0,n∈Z)时细菌的总数有多少个(用关于n的式子表示)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com