6．在函数在上是增函数，则的值可以是

　　　 A．1　　　　　　　　　　　　　 B．2　　　　　　　　　　　　　　 C．－1　　　　　　　　　　　　 D．－2

5、先将一个棱长为3的正方体木块的六个面分别涂上六种颜色，再将该正方体均匀割成棱长为1的小正方体，现从切好的小正方体中任取一块，所得正方体的六个面均没有涂色的概率是(　　 ).

　　　 A．　　 　　 B．　 　　 C． 　　　D．

4．若，其中a、b是虚数单位，则等于(　　 )

　　　 A．－3　 　　　 B．－1 　 　　　C．3　 　　　 D．1

3．在空间中，有如下四个命题：

　　　 ①平行于同一个平面的两条直线是平行直线，

　　　 ②垂直于同一条直线的两个平面是平行平面；

　　　 ③若平面内有不共线的三个点到平面距离相等，则//；

　　　 ④过平面的一条斜线有且只有一个平面与平面垂直。

其中正确的两个命题是

A．①、③　　　　　　 　　　 B．②、④　　　　　　　　　 C．①、④　　　　　　 　　　 D．②、③

2．将函数的图像按向量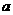平移后，得到的图像，则

　　　 A．　　　　　　　　　　 B．　　 　　　 C．　　　　　　 D．

1．已知集合,，那么集合等于

A．　　　　　　　　　　　　　　　　　　　　 B．

C．　　　　　　　　　　　　　　　　　 D．

(17)(本小题满分12分)

已知函数求使为正值的的集合

(18)(本小题满分12分)

设甲、乙、丙三台机器是否需要照顾相互之间没有影响已知在某一小时内，甲、乙都需要照顾的概率为0.05，甲、丙都需要照顾的概率为0.1，乙、丙都需要照顾的概率为0.125，

(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少；

(Ⅱ)计算这个小时内至少有一台需要照顾的概率　　　　

(19)(本小题满分12分)

在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，

　　 平面VAD⊥底面ABCD

　　 1)求证AB⊥面VAD；

　　 2)求面VAD与面VDB所成的二面角的大小

(20)(本小题满分12分)

在等差数列中，公差，是与的等差中项，已知数列,,,,……,,……成等比数列，求数列的通项

(21) (本小题满分12分)

用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?

(22) (本小题满分14分)

设两点在抛物线上，是AB的垂直平分线，

(Ⅰ)当且仅当取何值时，直线经过抛物线的焦点F？证明你的结论；

(Ⅱ)当时，求直线的方程

(13)经问卷调查，某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度，其中执“一般”态度的比“不喜欢”态度的多12人，按分层抽样方法从全班选出部分学生座谈摄影，如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学，那么全班学生中“喜欢”摄影的比全班人数的一半还多　　　　 人

(14)已知向量，且A、B、C三点共线，则k=　　

(15)曲线在点(1，1)处的切线方程为　　　　　　　

(16)已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是AB上的点，则点P到AC、BC的距离乘积的最大值是　　　　　　

(1)已知为第三象限角，则所在的象限是

　　 (A)第一或第二象限　　　　　　 (B)第二或第三象限

(C)第一或第三象限　　　　　　 (D)第二或第四象限

(2)已知过点A(-2，m)和B(m，4)的直线与直线2x+y-1=0平行，则m的值为

(A)0　　　　 (B)-8　　　　 (C)2　　　 (D)10

(3)在的展开式中的系数是

(A)-14　　 (B)14　　　　 (C)-28　　　 (D)28

(4)设三棱柱ABC-A₁B₁C₁的体积为V，P、Q分别是侧棱AA₁、CC₁上的点，且PA=QC₁，则四棱锥B-APQC的体积为

(A)　　 (B)　　　 (C)　　 (D)

(5)设，则

(A)-2<x<-1　　 (B)-3<x<-2　 (C)-1<x<0　　 (D)0<x<1

(6)若,则

(A)a<b<c　　　　 (B)c<b<a　　　　 (C)c<a<b　　　 (D)b<a<c

(7)设,且,则

(A) 　(B) (C) 　(D)

(8)

(A) 　(B)　 　　　(C) 1　　　 (D)

(9)已知双曲线的焦点为F₁、F₂，点M在双曲线上且则点M到x轴的距离为

(A)　　 (B)　　 (C)　　 (D)

(10)设椭圆的两个焦点分别为F_1、、F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是

(A)　　　 (B)　 (C)(D)

(11)不共面的四个定点到平面的距离都相等，这样的平面共有

(A)3个　　　　　　 (B)4个　　 (C)6个　　 (D)7个

(12)计算机中常用十六进制是逢16进1的计数制，采用数字0-9和字母A-F共16个计数符号，这些符号与十进制的数的对应关系如下表：

例如，用十六进制表示：E+D=1B，则A×B=

(A)6E　　　 (B)72　　　　 (C)5F　　　 (D)B0

(17)(本小题满分12分)

在,求

(1)

(2)若点

(18)(本小题满分12分)

设等比数列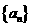的前n项和为，

(19)(本小题满分12分)

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验　 设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品　

(I)求取6件产品中有1件产品是二等品的概率　

(II)若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率　

(20)(本小题12分)

如图，在直三棱柱中，、分别为、的中点　

(I)证明：ED为异面直线与的公垂线；

(II)设求二面角的大小

　(21)(本小题满分为14分)

设，函数若的解集为A，，求实数的取值范围　

(22)(本小题满分12分)

已知抛物线的焦点为F，A、B是抛物线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M　

(I)证明为定值；

(II)设的面积为S，写出的表达式，并求S的最小值