
题目列表(包括答案和解析)
∴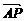 =
=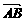 +
+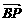 =a+m(μb-a)=(1-m)a+mμb ①
=a+m(μb-a)=(1-m)a+mμb ①
又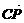 与
与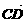 共线,∴
共线,∴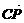 =n
=n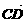 =n(
=n(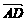 -
-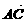 )=n(λa-b),
)=n(λa-b),
∴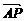 =
=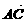 +
+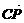 =b+n(λa-b)=nλa+(1-n)b ②
=b+n(λa-b)=nλa+(1-n)b ②
由①②,得(1-m)a+μmb=λna+(1-n)b.
∵a与b不共线,∴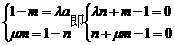 ③
③
解方程组③得:m=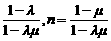 代入①式得c=(1-m)a+mμb=
代入①式得c=(1-m)a+mμb=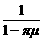 [λ(1-μ)a+μ(1-λ)b].
[λ(1-μ)a+μ(1-λ)b].
6.解:(1)以点A为坐标原点O,以AB所在直线为Oy轴,以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知,得A(0,0,0),B(0,a,0),A1(0,0,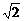 a),C1(-
a),C1(-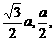
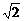 a).
a).
(2)取A1B1的中点M,于是有M(0,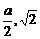 a),连AM,MC1,有
a),连AM,MC1,有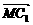 =(-
=(-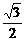 a,0,0),
a,0,0),
且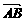 =(0,a,0),
=(0,a,0),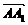 =(0,0
=(0,0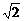 a)
a)
由于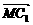 ·
·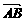 =0,
=0,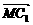 ·
·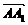 =0,所以MC1⊥面ABB1A1,∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
=0,所以MC1⊥面ABB1A1,∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵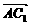 =
=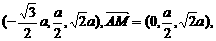
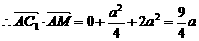
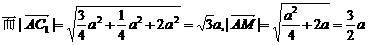
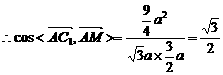
所以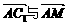 所成的角,即AC1与侧面ABB1A1所成的角为30°.
所成的角,即AC1与侧面ABB1A1所成的角为30°.
∴1·4+2·1=6≠0,∴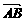 不垂直于
不垂直于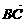 ,∴ABCD也不是矩形,故选D.
,∴ABCD也不是矩形,故选D.
答案:D
2.解析:∵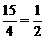 ·3·5sinα得sinα=
·3·5sinα得sinα=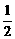 ,则α=30°或α=150°.
,则α=30°或α=150°.
又∵a·b<0,∴α=150°.
答案:C
8.已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的?中点.?
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明:BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有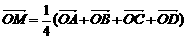 .参考答案
.参考答案
7.已知两点M(-1,0),N(1,0),且点P使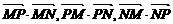 成公差小于零的等差数列.
成公差小于零的等差数列.
(1)点P的轨迹是什么曲线?
(2)若点P坐标为(x0,y0),Q为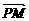 与
与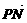 的夹角,求tanθ.
的夹角,求tanθ.
6.正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为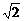 a.
a.
(1)建立适当的坐标系,并写出A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
5.如图,在△ABC中,设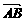 =a,
=a,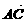 =b,
=b,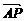 =c,
=c, 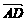 =λa,(0<λ<1),
=λa,(0<λ<1),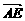 =μb(0<μ<1),试用向量a,b表示c.
=μb(0<μ<1),试用向量a,b表示c.
4.等腰△ABC和等腰Rt△ABD有公共的底边AB,它们所在的平面成60°角,若AB=16 cm,AC=17 cm,则CD=_________.
3.将二次函数y=x2的图象按向量a平移后得到的图象与一次函数y=2x-5的图象只有一个公共点(3,1),则向量a=_________.
2.已知△ABC中,?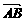 =a,
=a,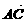 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=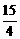 ,|a|=3,|b|=5,则a与b的夹角是( )
,|a|=3,|b|=5,则a与b的夹角是( )
A.30° B.-150° C.150° D.30°或150°
1.设A、B、C、D四点坐标依次是(-1,0),(0,2),(4,3),(3,1),则四边形ABCD为( )
A.正方形 B.矩形
C.菱形 D.平行四边形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com