
题目列表(包括答案和解析)
6.已知α、β是平面,m、n是直线,则下命题不正确的是
A.若m∥n , m⊥α, 则n⊥α B.若,m⊥α, m⊥β, 则α∥β
C.若m⊥α, m∥n, n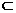 β, 则α⊥β D.若m∥α, α
∩β=n则m∥n
β, 则α⊥β D.若m∥α, α
∩β=n则m∥n
5.曲线y=2sin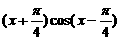 和直线在y=
和直线在y=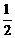 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于
A.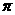 B.2
B.2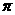 C.3
C.3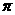 D.4
D.4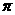
4.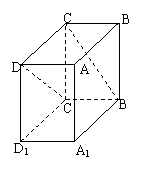 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为
A.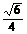 B.
B.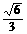
C.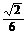 D.
D.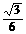
3.若函数f (x)= x3-x2-1,则此函数图象在点(1, f (1))处的切线的倾斜角为
A.0 B.锐角 C.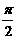 D.钝角
D.钝角
2.函数的y=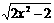 (x≤-1)反函数是
(x≤-1)反函数是
A.y=-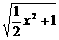 (x≥0) B.y=
(x≥0) B.y=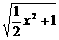 (x≥0)
(x≥0)
C.y=-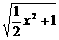 (x≥
(x≥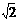 ) D.y=
) D.y=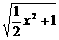 (x≥
(x≥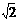 )
)
1.已知集合P={x|x2-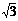 x<0},Q={x|
x<0},Q={x|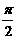 <x<
<x<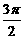 },则P∩Q=
},则P∩Q=
A.Φ B.{x|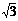 < x <
< x <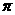 } C.{x|
} C.{x|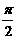 < x <
< x <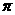 } D.{x|
} D.{x|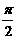 < x <
< x <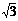 }
}
(三)解答题
17. 解: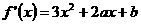 。
。
据题意,-1,3是方程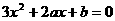 的两个根,由韦达定理得
的两个根,由韦达定理得
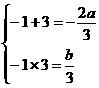
∴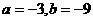
∴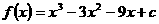
∵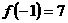 ,∴
,∴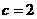
极小值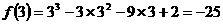
∴极小值为-25,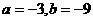 ,
,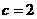 。
。
18. 解:(1)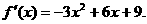 令
令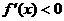 ,解得
,解得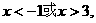
所以函数 的单调递减区间为
的单调递减区间为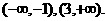
(2)因为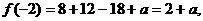
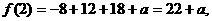
所以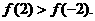 因为在(-1,3)上
因为在(-1,3)上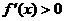 ,所以
,所以 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此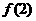 和
和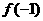 分别是
分别是 在区间
在区间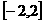 上的最大值和最小值.于是有
上的最大值和最小值.于是有 ,解得
,解得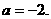
故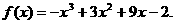 因此
因此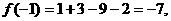
即函数 在区间
在区间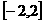 上的最小值为-7.
上的最小值为-7.
19. 解:(1)因为函数 ,
,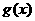 的图象都过点(
的图象都过点(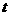 ,0),所以
,0),所以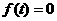 ,
,
即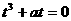 .因为
.因为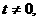 所以
所以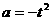 .
. 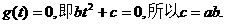
又因为 ,
,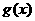 在点(
在点(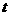 ,0)处有相同的切线,所以
,0)处有相同的切线,所以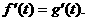
而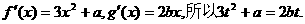
将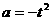 代入上式得
代入上式得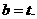 因此
因此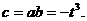 故
故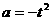 ,
,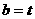 ,
,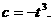
(2)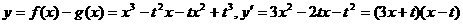 .
.
当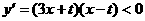 时,函数
时,函数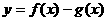 单调递减.
单调递减.
由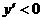 ,若
,若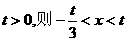 ;若
;若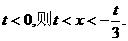
由题意,函数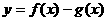 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则
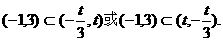 所以
所以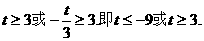
又当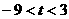 时,函数
时,函数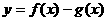 在(-1,3)上单调递减.
在(-1,3)上单调递减.
所以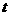 的取值范围为
的取值范围为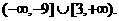
20. 解:(1)∵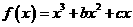 ,∴
,∴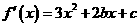 。从而
。从而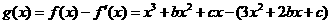 =
=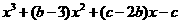 是一个奇函数,所以
是一个奇函数,所以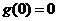 得
得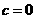 ,由奇函数定义得
,由奇函数定义得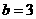 ;
;
(2)由(Ⅰ)知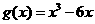 ,从而
,从而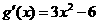 ,由此可知,
,由此可知,
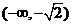 和
和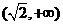 是函数
是函数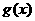 是单调递增区间;
是单调递增区间;
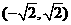 是函数
是函数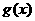 是单调递减区间;
是单调递减区间;
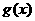 在
在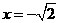 时,取得极大值,极大值为
时,取得极大值,极大值为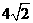 ,
,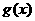 在
在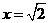 时,取得极小值,极小值为
时,取得极小值,极小值为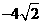 。
。
21. 解:设长方体的宽为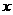 (m),则长为
(m),则长为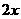 (m),高为
(m),高为
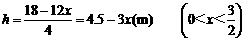 .
.
故长方体的体积为
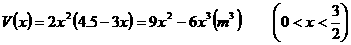
从而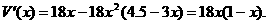
令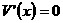 ,解得
,解得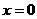 (舍去)或
(舍去)或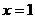 ,因此
,因此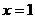 .
.
当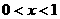 时,
时,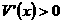 ;当
;当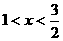 时,
时,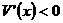 ,
,
故在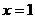 处
处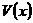 取得极大值,并且这个极大值就是
取得极大值,并且这个极大值就是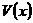 的最大值。
的最大值。
从而最大体积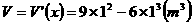 ,此时长方体的长为2 m,高为1.5 m.
,此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为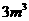 。
。
22. 解:(1)因为函数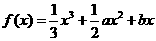 在区间
在区间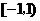 ,
,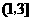 内分别有一个极值点,所以
内分别有一个极值点,所以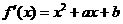
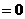 在
在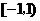 ,
,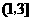 内分别有一个实根,
内分别有一个实根,
设两实根为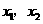 (
(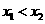 ),则
),则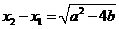 ,且
,且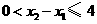 .于是
.于是
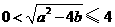 ,
,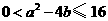 ,且当
,且当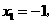
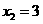 ,即
,即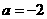 ,
,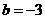 时等号成立.故
时等号成立.故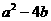 的最大值是16.
的最大值是16.
(2)解法一:由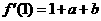 知
知 在点
在点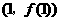 处的切线
处的切线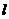 的方程是
的方程是
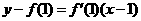 ,即
,即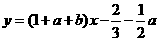 ,
,
因为切线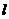 在点
在点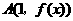 处空过
处空过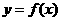 的图象,
的图象,
所以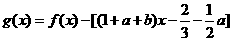 在
在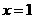 两边附近的函数值异号,则
两边附近的函数值异号,则
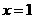 不是
不是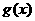 的极值点.
的极值点.
而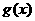
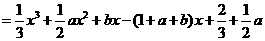 ,且
,且
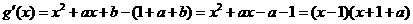 .
.
若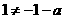 ,则
,则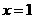 和
和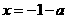 都是
都是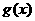 的极值点.
的极值点.
所以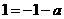 ,即
,即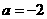 ,又由
,又由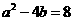 ,得
,得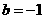 ,故
,故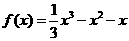 .
.
解法二:同解法一得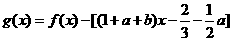
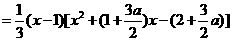 .
.
因为切线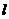 在点
在点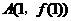 处穿过
处穿过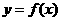 的图象,所以
的图象,所以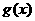 在
在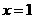 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在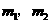 (
(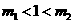 ).
).
当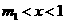 时,
时,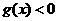 ,当
,当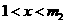 时,
时,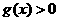 ;
;
或当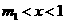 时,
时,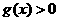 ,当
,当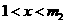 时,
时,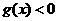 .
.
设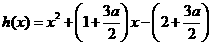 ,则
,则
当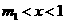 时,
时,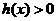 ,当
,当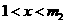 时,
时,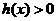 ;
;
或当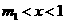 时,
时,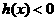 ,当
,当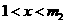 时,
时,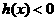 .
.
由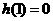 知
知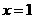 是
是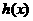 的一个极值点,则
的一个极值点,则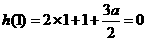 ,
,
所以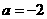 ,又由
,又由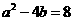 ,得
,得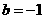 ,故
,故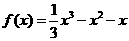 .
.
6 复习建议
重点是利用导数的几何意义求解与切线有关的综合性问题求解和多项式函数的导数。有意识地把导数函数的单调性、函数的极值、最值、二次函数、方程等进行交汇,综合运用。特别是精选一些以导数为工具分析和解决一些函数问题,以及一些实际问题中的最大(小)值问题。
(二)填空题
13. 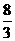 14.
14. 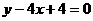 15. 7 16. 20
15. 7 16. 20
(一)选择题
1.A 2.B 3.D 4.A 5.D 6.D 7.A 8.A 9.A 10.A 11.D 12.A
(二)2008年高考预测
导数的考查方式以客观题为主,主要考查求导数的基本公式和法则,以及导数的几何意义。也可以解答题的形式出现,即以导数的几何意义为背景设置成导数与解析几何的综合题。导数的应用是重点,侧重于利用导数确定函数的单调性和极值、最值、值域问题。
4 强化训练
5 选择题
1. 已知曲线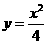 的一条切线的斜率为
的一条切线的斜率为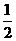 ,则切点的横坐标为(
A )
,则切点的横坐标为(
A )
A.1 B.2 C.3 D.4
2. 曲线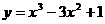 在点(1,-1)处的切线方程为 ( B )
在点(1,-1)处的切线方程为 ( B )
A.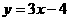 B.
B.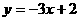 C.
C.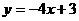 D.
D.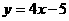
3. 函数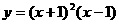 在
在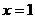 处的导数等于
( D
)
处的导数等于
( D
)
A.1 B.2 C.3 D.4
4. 已知函数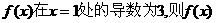 的解析式可能为 (
A )
的解析式可能为 (
A )
A.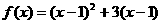 B.
B.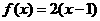
C.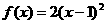 D.
D.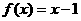
5. 函数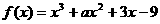 ,已知
,已知 在
在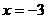 时取得极值,则
时取得极值,则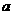 =( D )
=( D )
(A)2 (B)3 (C)4 (D)5
6. 函数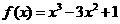 是减函数的区间为(
D )
是减函数的区间为(
D )
(A)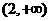 (B)
(B)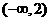 (C)
(C)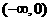 (D)
(D)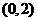
7. 若函数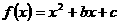 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数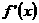 的图象是(
A )
的图象是(
A )
8. 函数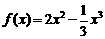 在区间
在区间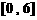 上的最大值是( A )
上的最大值是( A )
A.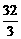 B.
B.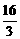 C.
C.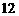 D.
D.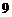
9. 函数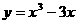 的极大值为
的极大值为 ,极小值为
,极小值为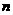 ,则
,则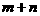 为 ( A )
为 ( A )
A.0 B.1 C.2 D.4
10. 三次函数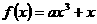 在
在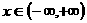 内是增函数,则 ( A )
内是增函数,则 ( A )
A. 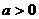 B.
B.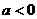 C.
C.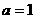 D.
D.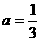
11. 在函数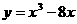 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于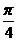 的点中,坐标为整数的点的个数是 ( D )
的点中,坐标为整数的点的个数是 ( D )
A.3 B.2 C.1 D.0
12. 函数 的定义域为开区间
的定义域为开区间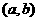 ,导函数
,导函数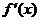 在
在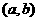 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间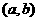 内有极小值点( A
)
内有极小值点( A
)
A.1个 B.2个
C.3个 D. 4个
2 填空题
13. 曲线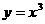 在点
在点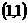 处的切线与
处的切线与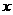 轴、直线
轴、直线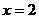 所围成的三角形的面积为__________。
所围成的三角形的面积为__________。
14. 已知曲线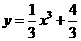 ,则过点
,则过点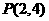 “改为在点
“改为在点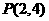 ”的切线方程是______________
”的切线方程是______________
15. 已知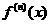 是对函数
是对函数 连续进行n次求导,若
连续进行n次求导,若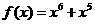 ,对于任意
,对于任意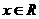 ,都有
,都有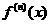 =0,则n的最少值为
。
=0,则n的最少值为
。
16. 某公司一年购买某种货物400吨,每次都购买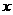 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为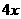 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则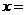 吨.
吨.
3 解答题
17. 已知函数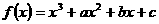 ,当
,当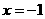 时,取得极大值7;当
时,取得极大值7;当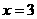 时,取得极小值.求这个极小值及
时,取得极小值.求这个极小值及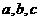 的值.
的值.
18. 已知函数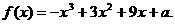
(1)求 的单调减区间;
的单调减区间;
(2)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
19. 设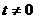 ,点P(
,点P(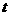 ,0)是函数
,0)是函数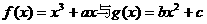 的图象的一个公共点,两函数的图象在点P处有相同的切线。
的图象的一个公共点,两函数的图象在点P处有相同的切线。
(1)用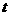 表示
表示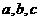 ;
;
(2)若函数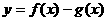 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求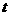 的取值范围。
的取值范围。
20. 设函数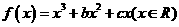 ,已知
,已知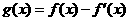 是奇函数。
是奇函数。
(1)求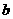 、
、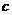 的值。
的值。
(2)求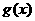 的单调区间与极值。
的单调区间与极值。
21. 用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
22. 已知函数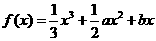 在区间
在区间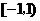 ,
,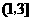 内各有一个极值点.
内各有一个极值点.
(1)求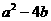 的最大值;
的最大值;
7
当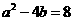 时,设函数
时,设函数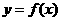 在点
在点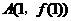 处的切线为
处的切线为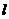 ,若
,若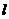 在点
在点 处穿过函数
处穿过函数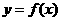 的图象(即动点在点
的图象(即动点在点 附近沿曲线
附近沿曲线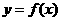 运动,经过点
运动,经过点 时,从
时,从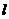 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数 的表达式.
的表达式.
强化训练答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com