
题目列表(包括答案和解析)
3.二次函数是初中、高中的结合点,应引起重视,复习时要适当加深加宽.二次函数与二次方程、二次不等式有着密切的联系,要沟通这些知识之间的内在联系,灵活运用它们去解决有关问题.
2.掌握函数图象的基本变换,如平移、翻转、对称等.
基本函数:一次函数、二次函数、反比例函数、指数函数与对数函数,它们的图象与性质是函数的基石.求反函数,判断、证明与应用函数的三大特性(单调性、奇偶性、周期性)是高考命题的切入点,有单一考查,也有综合考查.函数的图象、图象的变换是高考热点,应用函数知识解其他问题,特别是解应用题能很好地考查学生分析问题、解决问题的能力,这类问题在高考中具有较强的生存力.配方法、待定系数法、数形结合法、分类讨论等,这些方法构成了函数这一章应用的广泛性、解法的多样性和思维的创造性,这均符合高考试题改革的发展趋势.
特别在“函数”这一章中,数形结合的思想比比皆是,深刻理解和灵活运用这一思想方法,不仅会给解题带来方便,而且这正是充分把握住了中学数学的精髓和灵魂的体现.
复习本章要注意:
1.深刻理解一些基本函数,如二次函数、指数函数、对数函数的图象与性质,对数与形的基本关系能相互转化.
1解:依题意,有x1=50+x3-55=x3-5,\x1<x3,同理,x2=30+x1-20=x1+10\x1<x2,同理,x3=30+x2-35=x2-5\x3<x2故选C
2解:令c=π,则对任意的x∈R,都有f(x)+f(x−c)=2,于是取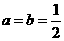 ,c=π,则对任意的x∈R,af(x)+bf(x−c)=1,由此得
,c=π,则对任意的x∈R,af(x)+bf(x−c)=1,由此得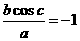 。选C。
。选C。
 17解:(1)
17解:(1)
(2)方程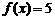 的解分别是
的解分别是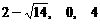 和
和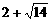 ,由于
,由于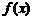 在
在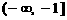 和
和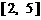 上单调递减,在
上单调递减,在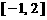 和
和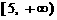 上单调递增,因此
上单调递增,因此
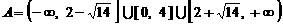 .
.
由于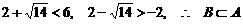 .
.
(3)[解法一] 当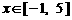 时,
时,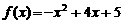 .
.
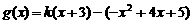
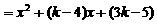
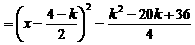 ,
,
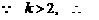
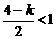 . 又
. 又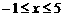 ,
,
① 当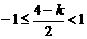 ,即
,即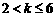 时,取
时,取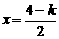 ,
,
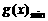
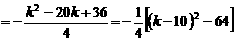 .
.
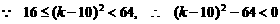 ,
,
则 .
.
② 当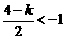 ,即
,即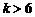 时,取
时,取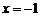 ,
, 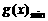 =
=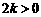 .
.
由 ①、②可知,当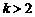 时,
时,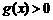 ,
,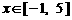 .
.
因此,在区间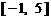 上,
上,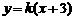 的图像位于函数
的图像位于函数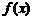 图像的上方.
图像的上方.
[解法二] 当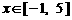 时,
时,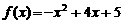 .
.
由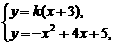 得
得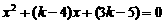 ,
,
令 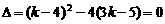 ,解得
,解得 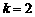 或
或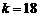 ,
,
在区间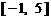 上,当
上,当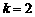 时,
时,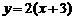 的图像与函数
的图像与函数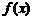 的图像只交于一点
的图像只交于一点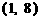 ; 当
; 当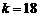 时,
时,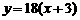 的图像与函数
的图像与函数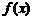 的图像没有交点.
的图像没有交点.
如图可知,由于直线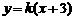 过点
过点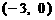 ,当
,当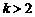 时,直线
时,直线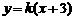 是由直线
是由直线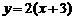 绕点
绕点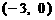 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间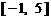 上,
上,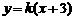 的图像位于函数
的图像位于函数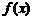 图像的上方.
图像的上方.
18解:(I)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,x∈[-5,5]
∴x=1时,f(x)的最小值为1
x=-5时,f(x)的最大值为37
(II)函数f(x)=(x+a)2+2-a2图象的对称轴为x=-a
∵f(x)在区间[-5,5]上是单调函数
∴-a≤-5或-a≥5
故a的取值范围是a≤-5或a≥5.
19解:(Ⅰ)因为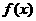 是奇函数,所以
是奇函数,所以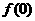 =0,即
=0,即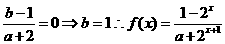
又由f(1)= -f(-1)知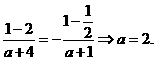
(Ⅱ)解法一:由(Ⅰ)知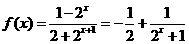 ,易知
,易知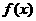 在
在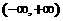 上
上
为减函数。又因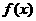 是奇函数,从而不等式:
是奇函数,从而不等式: 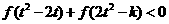
等价于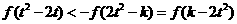 ,因
,因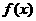 为减函数,由上式推得:
为减函数,由上式推得:
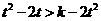 .即对一切
.即对一切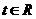 有:
有: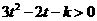 ,
,
从而判别式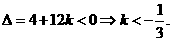
解法二:由(Ⅰ)知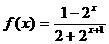 .又由题设条件得:
.又由题设条件得: 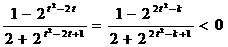 ,
,
即 :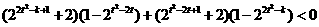 ,
,
整理得 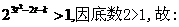
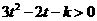
上式对一切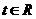 均成立,从而判别式
均成立,从而判别式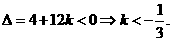
20解:(Ⅰ)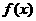 的定义域为
的定义域为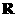 ,
,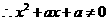 恒成立,
恒成立,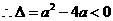 ,
,
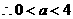 ,即当
,即当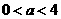 时
时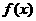 的定义域为
的定义域为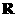 .
.
(Ⅱ)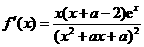 ,令
,令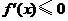 ,得
,得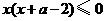 .
.
由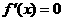 ,得
,得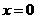 或
或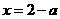 ,又
,又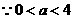 ,
,
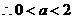 时,由
时,由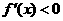 得
得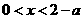 ;
;
当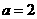 时,
时,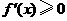 ;当
;当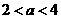 时,由
时,由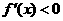 得
得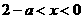 ,
,
即当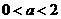 时,
时,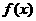 的单调减区间为
的单调减区间为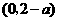 ;
;
当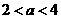 时,
时,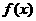 的单调减区间为
的单调减区间为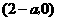 .
.
21解:(Ⅰ)设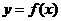 与
与 在公共点
在公共点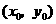 处的切线相同.
处的切线相同.
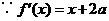 ,
,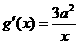 ,由题意
,由题意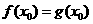 ,
,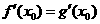 .
.
即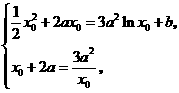 由
由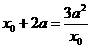 得:
得: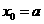 ,或
,或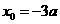 (舍去).
(舍去).
即有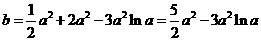 .
.
令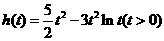 ,则
,则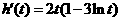 .于是
.于是
当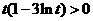 ,即
,即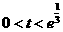 时,
时,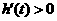 ;
;
当 ,即
,即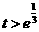 时,
时,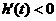 .
.
故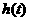 在
在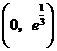 为增函数,在
为增函数,在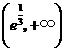 为减函数,
为减函数,
于是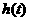 在
在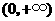 的最大值为
的最大值为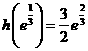 .
.
(Ⅱ)设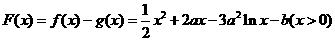 ,
,
则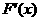
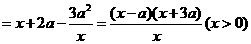 .
.
故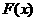 在
在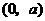 为减函数,在
为减函数,在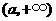 为增函数,
为增函数,
于是函数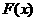 在
在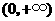 上的最小值是
上的最小值是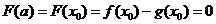 .
.
故当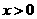 时,有
时,有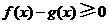 ,即当
,即当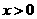 时,
时,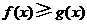 .
.
22解析:(1)∵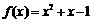 ,
,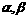 是方程f(x)=0的两个根
是方程f(x)=0的两个根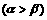 ,
,
∴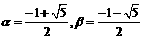 ;
;
(2)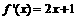 ,
,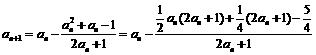
=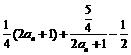 ,∵
,∵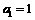 ,∴有基本不等式可知
,∴有基本不等式可知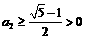 (当且仅当
(当且仅当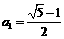 时取等号),∴
时取等号),∴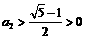 同,样
同,样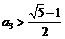 ,……,
,……,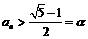 (n=1,2,……),
(n=1,2,……),
(3)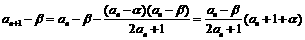 ,而
,而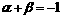 ,即
,即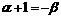 ,
,
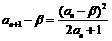 ,同理
,同理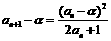 ,
,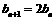 ,又
,又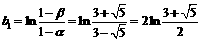
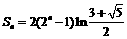
13解:由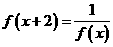 得
得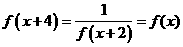 ,所以
,所以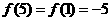 ,则
,则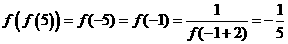 。
。
14解: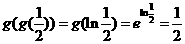 .
.
15解:函数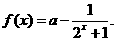 若
若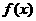 为奇函数,则
为奇函数,则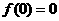 ,即
,即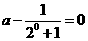 ,a=
,a=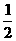 .
.
16解:由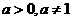 ,函数
,函数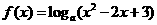 有最小值可知a>1,所以不等式
有最小值可知a>1,所以不等式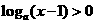 可化为x-1>1,即x>2.
可化为x-1>1,即x>2.
1解:找到原函数的定义域和值域,x∈[0,+∞),y∈(1,2)
又∵原函数的值域是反函数的定义域,
∴反函数的定义域x∈(1,2),∴C、D不对.
而1<x<2,∴0<x-1<1,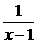 >1.
>1.
又log2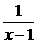 >0,即y>0∴A正确.
>0,即y>0∴A正确.
2解:依题意,有0<a<1且3a-1<0,解得0<a<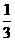 ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³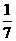 故选C
故选C
3解: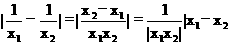 |
|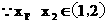
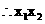 >1
>1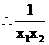 <1\
<1\ 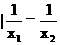 |<|x1-x2|故选A
|<|x1-x2|故选A
4解:已知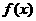 是周期为2的奇函数,当
是周期为2的奇函数,当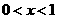 时,
时,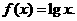 设
设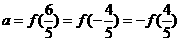 ,
,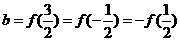 ,
,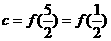 <0,∴
<0,∴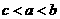 ,选D.
,选D.
5解:由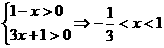 ,故选B.
,故选B.
6解:B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇函数,是减函数;故选A.
7解: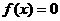 的根是
的根是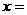 2,故选C
2,故选C
8解:A中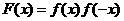 则
则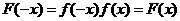 ,
,
即函数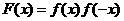 为偶函数,B中
为偶函数,B中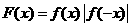 ,
,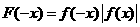 此时
此时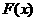 与
与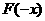 的关系不能确定,即函数
的关系不能确定,即函数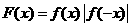 的奇偶性不确定,
的奇偶性不确定,
C中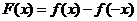 ,
,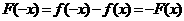 ,即函数
,即函数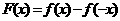 为奇函数,D中
为奇函数,D中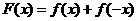 ,
,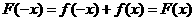 ,即函数
,即函数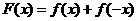 为偶函数,故选择答案D。
为偶函数,故选择答案D。
9解:函数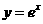 的图象与函数
的图象与函数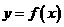 的图象关于直线
的图象关于直线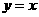 对称,所以
对称,所以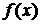 是
是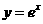 的反函数,即
的反函数,即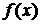 =
= ,∴
,∴ 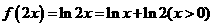 ,选D.
,选D.
10解:f(f(2))=f(1)=2,选C
11解:当x<-1时,|x+1|=-x-1,|x-2|=2-x,因为(-x-1)-(2-x)=-3<0,所以2-x>-x-1;当-1£x<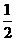 时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当
时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当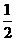 £x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
£x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
故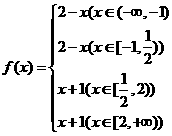 据此求得最小值为
据此求得最小值为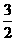 。选C
。选C
12解:关于x的方程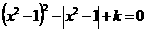 可化为
可化为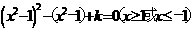 …(1)
…(1)
或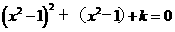 (-1<x<1)…………(2)
(-1<x<1)…………(2)
①
当k=-2时,方程(1)的解为±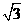 ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根
②
当k=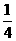 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根±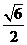 ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根±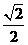 ,即原方程恰有4个不同的实根
,即原方程恰有4个不同的实根
③
当k=0时,方程(1)的解为-1,+1,±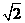 ,方程(2)的解为x=0,原方程恰有5个不同的实根
,方程(2)的解为x=0,原方程恰有5个不同的实根
④
当k=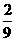 时,方程(1)的解为±
时,方程(1)的解为±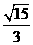 ,±
,±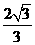 ,方程(2)的解为±
,方程(2)的解为±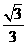 ,±
,±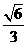 ,即原方程恰有8个不同的实根
,即原方程恰有8个不同的实根
选A
(四) 创新试题
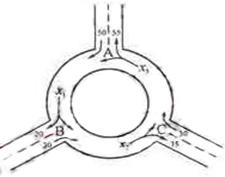
1. 下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口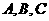 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中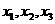 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段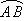 、
、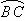 、
、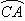 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)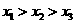 (B)
(B)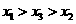 (C)
(C)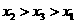 (D)
(D)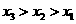
2. 设函数f(x)=3sinx+2cosx+1。若实数a、b、c使得af(x)+bf(x−c)=1对任意实数x恒成立,则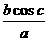 的值等于( )
的值等于( )
A. 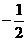 B.
B. 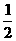 C. −1 D. 1
C. −1 D. 1
解答:
(三) 解答题
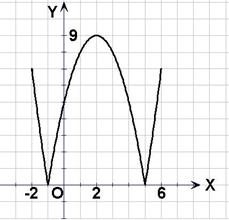
17. 设函数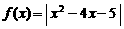 .
.
(1)在区间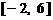 上画出函数
上画出函数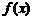 的图像;
的图像;
(2)设集合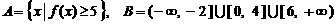 . 试判断集合
. 试判断集合 和
和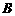 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当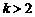 时,求证:在区间
时,求证:在区间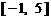 上,
上,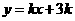 的图像位于函数
的图像位于函数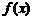 图像的上方.
图像的上方.
18、已知函数f(x)=x2+2ax+2,x∈[-5,5]
(I)当a=-1时,求函数f(x)的最大值和最小值;
(II)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
19. 已知定义域为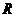 的函数
的函数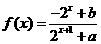 是奇函数。
是奇函数。
(Ⅰ)求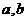 的值;
的值;
(Ⅱ)若对任意的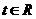 ,不等式
,不等式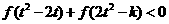 恒成立,求
恒成立,求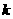 的取值范围;
的取值范围;
20.设函数f(x)=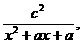 其中a为实数.
其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时,求f(x)的单减区间.
21. 已知定义在正实数集上的函数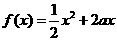 ,
,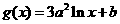 ,其中
,其中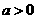 .设两曲线
.设两曲线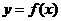 ,
,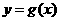 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用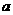 表示
表示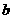 ,并求
,并求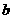 的最大值;
的最大值;
(II)求证: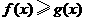 (
(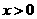 ).
).
22. 已知函数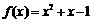 ,
,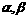 是方程f(x)=0的两个根
是方程f(x)=0的两个根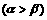 ,
,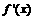 是f(x)的导数;设
是f(x)的导数;设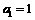 ,
,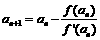 (n=1,2,……)
(n=1,2,……)
(1)求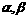 的值;
的值;
(2)证明:对任意的正整数n,都有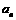 >a;
>a;
(3)记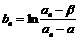 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。
(二) 填空题
13.函数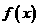 对于任意实数
对于任意实数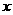 满足条件
满足条件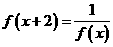 ,若
,若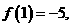 则
则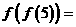 _______________。
_______________。
14.设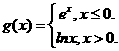 则
则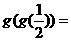 __________
__________
15.已知函数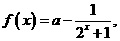 ,若
,若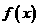 为奇函数,则
为奇函数,则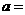 ________。
________。
16. 设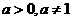 ,函数
,函数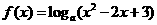 有最小值,则不等式
有最小值,则不等式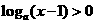 的解集为
。
的解集为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com