
题目列表(包括答案和解析)
15、已知:|a|=5,|b|=4,且a与b的夹角为60°,问当且仅当k为何值时,向量ka-b与 a+2b
垂直?
解: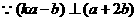
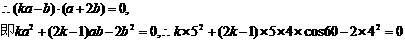
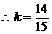 .
.
[平面向量的综合应用练习]
14、四边形ABCD中,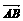 = a,
= a, 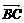 = b,
= b,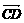 = c,
= c,
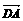 = d,且a·b=b·c=c·d=d
·a,判断四边形ABCD是什么图形?
= d,且a·b=b·c=c·d=d
·a,判断四边形ABCD是什么图形?
分析:在四边形ABCD中,a+b+c+d=0,这是一个隐含条件,
对a+b=-(c+d),两边平方后,用a·b=b·c=d·c代入,
从四边形的边长与内角的情况来确定四边形的形状.
解:∵a+b+c+d=0,∴a+b=-(c+d),
∴(a+b)2=(c+d)2,即|a|2+2a·b+|b|2=|c|2+2c·d+|d|2,
∵a·b=c·d,∴|a|2+|b|2=|c|2+|d|2……①
同理:|a|2+|d|2=|b|2+|c|2……②
①,②两式相减得:|b|2=|d|2,|a|2=|c|2,即|b|=|d|,|a|=|c|.
∴ABCD为平行四边形.
又∵a·b=b·c,即b·(a-c)=0,而a=-c,
∵b·(2a)=0
∴a⊥b,
∴四边形ABCD为矩形.
13、已知| a|=4,|b|=5,|a+b|=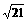 ,求:① a·b ;②(2a-b) ·(a+3b)
,求:① a·b ;②(2a-b) ·(a+3b)
解:①|a+b|2=(a+b)2=a2+2ab+b2=|a|2+2a·b+|b|2,
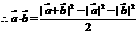 =
=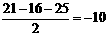 .
.
②(2a-b)·(a+3b)=2a2+5a·b-3b2=2|a|2+5a·b-3|b|2
=2×42+5×(-10)-3×52=-93.
12、 a与d=b-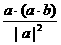 关系为________. a⊥b
关系为________. a⊥b
11、|a|=5, |b|=3,|a-b|=7,则a、b的夹角为__________. 120°
10、设a=(m+1)i-3j, b=i+(m-1)j, (a+b) ⊥(a-b), 则m=________.-2
9、已知e是单位向量,求满足a∥e且a·e=-18的向量a=__________.-18e
8、设 a,b,c是平面内任意的非零向量且相互不共线,则( D )
①(ab)c-(ca)b=0 ②|a| -|b|< |a-b|
③(bc)a-(ca)b不与c垂直 ④(3a+2b)(3a-2b)= 9|a|2-4|b|2
其中真命题是 ( )
A.①② B.②③ C.③④ D.②④
7、己知|a|=1,|b|=2, a与b的夹角为600,c =3a+b, d =λa-b ,若c⊥d,则实数λ的值为( C )
A. 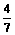 B.
B.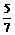 C.
C.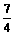 D.
D.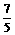
6、设|a|= 4,|b|= 3, 夹角为60°, 则|a+b|等于( C )
A.37
B.13 C.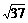 D.
D.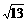
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com