
题目列表(包括答案和解析)
5、若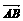 ·
·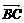 +
+ 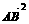 = 0,则ΔABC为( A )
= 0,则ΔABC为( A )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.等腰直角三角形
4、已知|a|=1,|b|=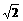 ,且(a-b)和a垂直,则a与b的夹角为( D
)
,且(a-b)和a垂直,则a与b的夹角为( D
)
A.60° B.30° C.135° D.45°
3、若|a|=|b|=|a-b|,则b与a+b的夹角为( A )
A.30° B.60° C.150° D.120°
2、在ΔABC中,若(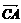 +
+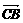 )·(
)·(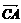 -
-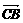 )=0,则ΔABC为( C
)
)=0,则ΔABC为( C
)
A.正三角形 B.直角三角形 C.等腰三角形 D.无法确定
1、下列各式中正确的是( C )
(1)(λ·a) ·b=λ·(a b)=a· (λb), (2)|a·b|=|a|·|b|,
(3)(a ·b)· c=a · (b ·c), (4)(a+b) · c= a·c+b·c
A.(1)(3) B.(2)(4) C.(1)(4) D.以上都不对.
[平面向量练习]
7.利用向量的数量积解决有关不等式、最值问题.
[例10]
证明柯西不等式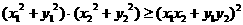
证明:令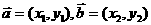
(1)
当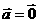 或
或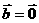 时,
时,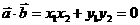 ,结论显然成立;
,结论显然成立;
(2)
当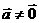 且
且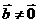 时,令
时,令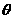 为
为 的夹角,则
的夹角,则

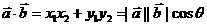 . 又
. 又

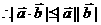 (当且仅当
(当且仅当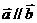 时等号成立)
时等号成立)
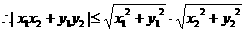

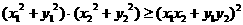 .(当且仅当
.(当且仅当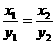 时等号成立)
时等号成立)
[例11]
求 的最值
的最值
解:原函数可变为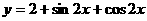 ,
,
所以只须求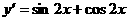 的最值即可,
的最值即可,
构造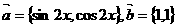 ,
,
那么 .
.
故 .
.
[例12] 三角形ABC中,A(5,-1)、B(-1,7)、C(1,2),求:(1)BC边上的中线
AM的长;(2)∠CAB的平分线AD的长;(3)cosABC的值.
解:(1)点M的坐标为xM=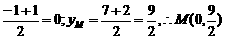

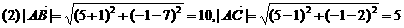
D点分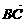 的比为2.
的比为2.
∴xD=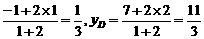
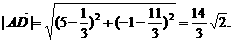
(3)∠ABC是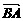 与
与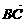 的夹角,而
的夹角,而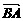 =(6,8),
=(6,8),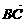 =(2,-5).
=(2,-5).

解斜三角形
[例1]
已知△ABC的三个内角A、B、C满足A+C=2B.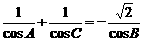 ,求cos
,求cos 的值.
的值.
解法一:由题设条件知B=60°,A+C=120°.
设α= ,则A-C=2α,可得A=60°+α,C=60°-α,
,则A-C=2α,可得A=60°+α,C=60°-α,

依题设条件有
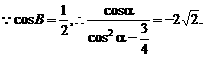
整理得4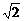 cos2α+2cosα-3
cos2α+2cosα-3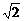 =0(M)
=0(M)
(2cosα-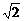 )(2
)(2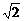 cosα+3)=0,∵2
cosα+3)=0,∵2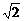 cosα+3≠0,
cosα+3≠0,
∴2cosα-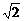 =0.从而得cos
=0.从而得cos .
.
解法二:由题设条件知B=60°,A+C=120°
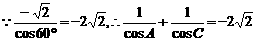 ①,把①式化为cosA+cosC=-2
①,把①式化为cosA+cosC=-2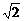 cosAcosC ②,
cosAcosC ②,
利用和差化积及积化和差公式,②式可化为
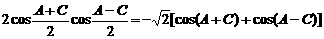 ③,
③,
将cos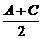 =cos60°=
=cos60°=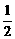 ,cos(A+C)=-
,cos(A+C)=-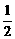 代入③式得:
代入③式得:
 ④
④
将cos(A-C)=2cos2( )-1代入
④:4
)-1代入
④:4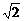 cos2(
cos2( )+2cos
)+2cos -3
-3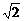 =0,(*),
=0,(*),
[例2]
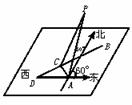 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为60°的B处,到11时10分又测得该船在岛北60°西、俯角为30°的C处。
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为60°的B处,到11时10分又测得该船在岛北60°西、俯角为30°的C处。
(1)求船的航行速度是每小时多少千米;
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
解:(1)在Rt△PAB中,∠APB=60° PA=1,∴AB=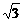 (千米)
(千米)
在Rt△PAC中,∠APC=30°,∴AC=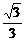 (千米)
(千米)
在△ACB中,∠CAB=30°+60°=90°
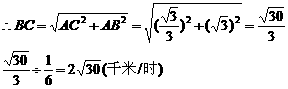
(2)∠DAC=90°-60°=30°
sinDCA=sin(180°-∠ACB)=sinACB=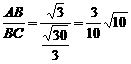
sinCDA=sin(∠ACB-30°)=sinACB·cos30°-cosACB·sin30° .
.
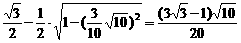
在△ACD中,据正弦定理得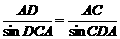 ,
,
∴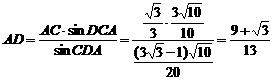
答:此时船距岛A为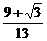 千米.
千米.
[例3]
已知△ABC的三内角A、B、C满足A+C=2B,设x=cos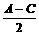 ,f(x)=cosB(
,f(x)=cosB(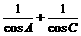 ).
).
(1)试求函数f(x)的解析式及其定义域;
(2)判断其单调性,并加以证明;
(3)求这个函数的值域.
解:(1)∵A+C=2B,∴B=60°,A+C=120°

∵0°≤| |<60°,∴x=cos
|<60°,∴x=cos ∈(
∈(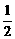 ,1
,1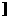
又4x2-3≠0,∴x≠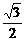 ,∴定义域为(
,∴定义域为(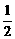 ,
,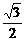 )∪(
)∪(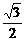 ,1].
,1].
(2)设x1<x2,∴f(x2)-f(x1)=
= ,若x1,x2∈(
,若x1,x2∈(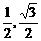 ),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
即f(x2)<f(x1),若x1,x2∈(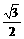 ,1],则4x12-3>0.
,1],则4x12-3>0.
4x22-3>0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0.
即f(x2)<f(x1),∴f(x)在(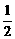 ,
,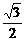 )和(
)和(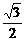 ,1
,1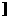 上都是减函数.
上都是减函数.
(3)由(2)知,f(x)<f(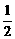 )=-
)=-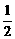 或f(x)≥f(1)=2.
或f(x)≥f(1)=2.
故f(x)的值域为(-∞,-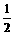 )∪[2,+∞
)∪[2,+∞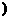 .
.
[例4]
在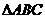 中,角
中,角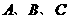 所对的边分别为
所对的边分别为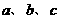 .若
.若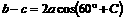 ,求角
,求角 .
.
解:由正弦定理,将已知等式中的边转化为角.可得
 .
.
因为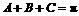 ,故有
,故有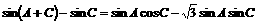 ,
,
∴
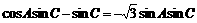 .
.
又∵ 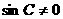 ,
,
∴ 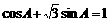 ,
,
即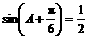 ,
,
由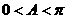 ,可解得
,可解得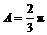 .
.
[例5]
在△ABC中,已知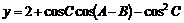 .
.
(1)若任意交换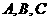 的位置,
的位置,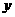 的值是否会发生变化?试证明你的结论;
的值是否会发生变化?试证明你的结论;
(2)求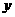 的最大值.
的最大值.
解:(1)∵
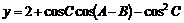

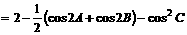
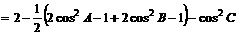

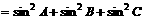 ,
,
∴ 任意交换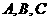 的位置,
的位置,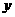 的值不会发生变化.
的值不会发生变化.
(2)
解法1:将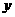 看作是关于
看作是关于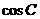 的二次函数.
的二次函数.
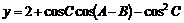
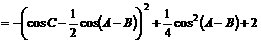 .
.
所以,当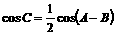 ,且
,且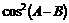 取到最大值1时,也即
取到最大值1时,也即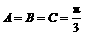 时,
时,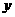 取得最大值
取得最大值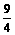 .
.
解法2:用调整的方法, 也即对于每个固定的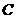 的值,去调整
的值,去调整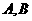 ,求出
,求出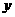 取得最大值时
取得最大值时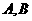 所满足的条件.
所满足的条件.
对于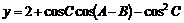 ,如果固定
,如果固定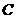 ,则可将
,则可将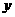 看作是关于
看作是关于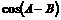 的一次或常数函数.为了讨论其最大值,显然应该考虑
的一次或常数函数.为了讨论其最大值,显然应该考虑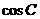 的符号,并由此展开讨论.
的符号,并由此展开讨论.
若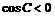 ,则
,则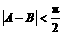 ,所以,
,所以,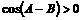 ,所以,
,所以,
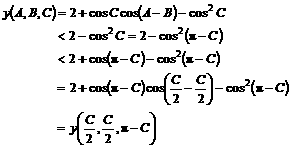
所以,只需考虑 的情形.此时
的情形.此时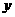 是关于
是关于 的常数函数或单调递增的一次函数,因此,最大值必可在
的常数函数或单调递增的一次函数,因此,最大值必可在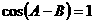 (即
(即 )时取得.所以,
)时取得.所以,
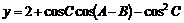
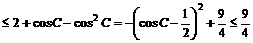 ,
,
等号当且仅当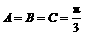 时取得.
时取得.
6.利用向量的数量积解决线与线的夹角及面与面的夹角问题.
[例9]
 证明:
证明:
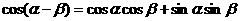
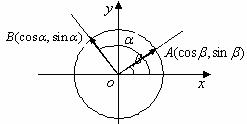
证明:在单位圆 上任取两点
上任取两点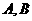 ,以
,以 为始边,以
为始边,以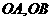 为终边的角分别为
为终边的角分别为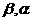 ,则
,则 点坐标为
点坐标为
 点坐标为
点坐标为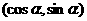 ;
;
则向量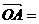

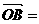
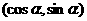 ,它们的夹角为
,它们的夹角为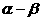 ,
,
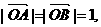
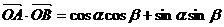 ,由向量夹角公式得:
,由向量夹角公式得:
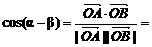
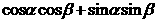 ,从而得证.
,从而得证.
注:用同样的方法可证明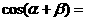
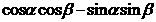
5.利用向量的数量积解决有关距离的问题,距离问题包括点到点的距离,点的线的距离,点到面的距离,线到线的距离,线到面的距离,面到面的距离.
[例8]
求平面内两点 间的距离公式
间的距离公式
解:设点 ,
,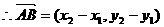
 ,而
,而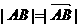
 点
点 与点
与点 之间的距离为:
之间的距离为:
4.利用向量的数量积解决两直线垂直问题
[例6]
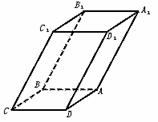 如图,已知平行六面体ABCD-A1B1C1D1的底面?ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
如图,已知平行六面体ABCD-A1B1C1D1的底面?ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)求证:C1C⊥BD.
(2)当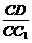 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
(1)证明:设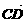 =a,
=a, 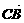 =b,
=b, =c,依题意,|a|=|b|,
=c,依题意,|a|=|b|,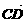 、
、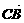 、?
、? 中两两所成夹角为θ,于是
中两两所成夹角为θ,于是 =a-b,
=a-b,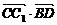 =c(a-b)=c·a-c·b=|c|·|a|cosθ-|c|·|b|cosθ=0,∴C1C⊥BD.
=c(a-b)=c·a-c·b=|c|·|a|cosθ-|c|·|b|cosθ=0,∴C1C⊥BD.
(2)解:若使A1C⊥平面C1BD,只须证A1C⊥BD,A1C⊥DC1,
由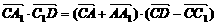
=(a+b+c)·(a-c)=|a|2+a·b-b·c-|c|2=|a|2-|c|2+|b|·|a|cosθ-|b|·|c|·cosθ=0,得
当|a|=|c|时,A1C⊥DC1,同理可证当|a|=|c|时,A1C⊥BD,
∴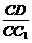 =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.
[例7]
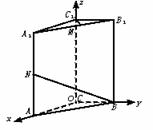 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.
(1)求 的长;
的长;
(2)求cos<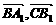 >的值;
>的值;
(3)求证:A1B⊥C1M.
解:(1)如图,以C为原点建立空间直角坐标系O-xyz.
依题意得:B(0,1,0),N(1,0,1)
∴| |=
|=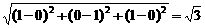 .
.
(2)解:依题意得:A1(1,0,2),C(0,0,0),B1(0,1,2).
∴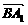 =
=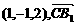 =(0,1,2)
=(0,1,2)
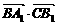 =1×0+(-1)×1+2×2=3
=1×0+(-1)×1+2×2=3
|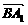 |=
|=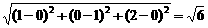

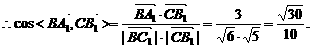
(3)证明:依题意得:C1(0,0,2),M(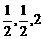 )
)
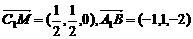
∴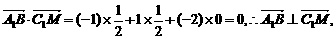
∴A1B⊥C1M.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com