
题目列表(包括答案和解析)
20. (本题满分14分)
已知二次函数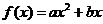 满足条件:
满足条件:
① 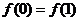 ; ②
; ② 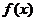 的最小值为
的最小值为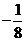 .
.
(1) 求函数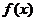 的解析式;
的解析式;
(2) 设数列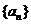 的前
的前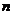 项积为
项积为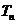 , 且
, 且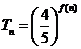 , 求数列
, 求数列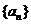 的通项公式;
的通项公式;
(3) 在(2)的条件下, 若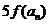 是
是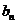 与
与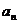 的等差中项, 试问数列
的等差中项, 试问数列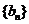 中第几项的值最小? 求出这个最小值.
中第几项的值最小? 求出这个最小值.


19. (本题满分14分)
已知集合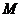 是满足下列性质的函数
是满足下列性质的函数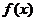 的全体, 存在非零常数
的全体, 存在非零常数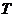 , 对任意
, 对任意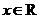 , 有
, 有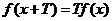 成立.
成立.
(1) 函数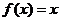 是否属于集合
是否属于集合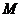 ? 说明理由;
? 说明理由;
(2) 设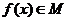 , 且
, 且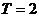 , 已知当
, 已知当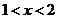 时,
时, 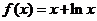 , 求当
, 求当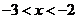 时,
时, 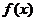 的解析式.
的解析式.
18.(本题满分14分)
设某物体一天中的温度T是时间t的函数,已知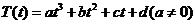 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
17. (本题满分14分)
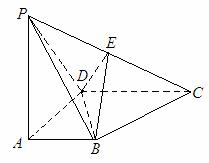 如图所示, 四棱锥P
如图所示, 四棱锥P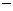 ABCD底面是直角梯形,
ABCD底面是直角梯形, 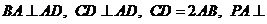 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明:
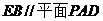 ;
;
(2)证明:
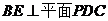 ;
;
(3)求三棱锥B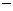 PDC的体积V.
PDC的体积V.
16. (本题满分12分)
设等比数列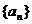 的公比为
的公比为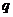 , 前
, 前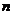 项和为
项和为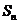 , 若
, 若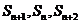 成等差数列, 求
成等差数列, 求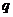 的值.
的值.
15. (本题满分12分)
已知向量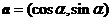 ,
, 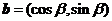 ,
, 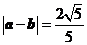 .
.
(Ⅰ)求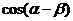 的值;
的值;
(Ⅱ)若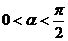 ,
, 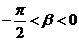 , 且
, 且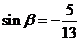 , 求
, 求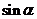 .
.
14. 甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是
甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是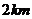 . 如图表示甲从家出发到乙同学家为止经过的路程
. 如图表示甲从家出发到乙同学家为止经过的路程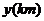 与时间
与时间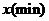 的关系, 其中甲在公园休息的时间是
的关系, 其中甲在公园休息的时间是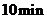 , 那么
, 那么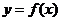 的表达式为
.
的表达式为
.
第Ⅱ卷(解答题共80分)
13. 要得到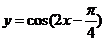 的图象, 且使平移的距离最短, 则需将
的图象, 且使平移的距离最短, 则需将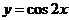 的图象向 方向平移
个单位即可得到.
的图象向 方向平移
个单位即可得到.
12. 设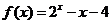 ,
, 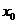 是函数
是函数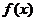 的一个正数零点, 且
的一个正数零点, 且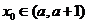 , 其中
, 其中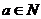 , 则
, 则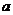 =
.
=
.
11. 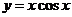 在
在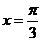 处的导数值是___________.
处的导数值是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com