
题目列表(包括答案和解析)
8.在正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,在这种情况下,若要使AD最小,求AD∶AB的值.
7.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a、b、3c成等比数列,又∠A-∠C=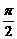 ,试求∠A、∠B、∠C的值.
,试求∠A、∠B、∠C的值.
6.在△ABC中,a、b、c分别为角A、B、C的对边,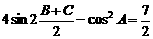 .
.
(1)求角A的度数;
(2)若a=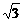 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
5.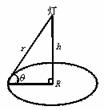 如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·
如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·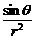 ,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
4.已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
3.在△ABC中,A为最小角,C为最大角,已知cos(2A+C)=-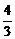 ,sinB=
,sinB=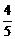 ,则cos2(B+C)=__________.
,则cos2(B+C)=__________.
2.在△ABC中,已知A、B、C成等差数列,则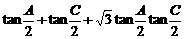 的值为__________.
的值为__________.
1.给出四个命题:(1)若sin2A=sin2B,则△ABC为等腰三角形;(2)若sinA=cosB,则△ABC为直角三角形;(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.以上正确命题的个数是( )
A.1 B.2 C.3 D.4
8.证明:(1)连结BG,则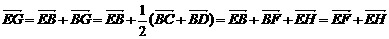
由共面向量定理的推论知:E、F、G、H四点共面,(其中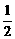
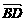 =
=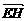 )
)
(2)因为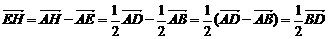 .
.
所以EH∥BD,又EH 面EFGH,BD
面EFGH,BD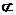 面EFGH
面EFGH
所以BD∥平面EFGH.
(3)连OM,OA,OB,OC,OD,OE,OG
由(2)知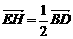 ,同理
,同理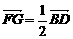 ,所以
,所以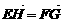 ,EH
,EH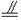 FG,所以EG、FH交于一点M且被M平分,所以
FG,所以EG、FH交于一点M且被M平分,所以
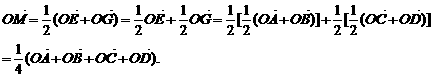 .
.
[解斜三角形练习]
7.解:(1)设P(x,y),由M(-1,0),N(1,0)得,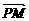 =-
=-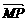 =(-1-x,-y),
=(-1-x,-y),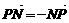 =(1-x,-y),
=(1-x,-y),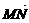 =-
=-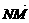 =(2,0),∴
=(2,0),∴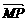 ·
·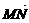 =2(1+x),
=2(1+x), 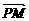 ·
·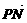 =x2+y2-1,
=x2+y2-1,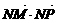 =2(1-x).于是,
=2(1-x).于是,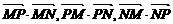 是公差小于零的等差数列,等价于
是公差小于零的等差数列,等价于
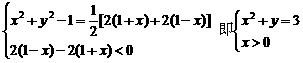
所以,点P的轨迹是以原点为圆心,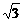 为半径的右半圆.
为半径的右半圆.
(2)点P的坐标为(x0,y0)
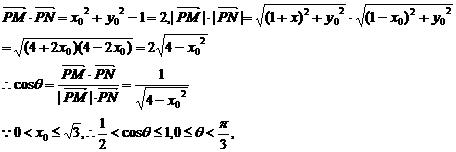
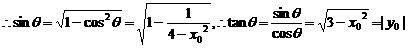
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com