
题目列表(包括答案和解析)
3、理解组合的意义,掌握组合数计算公式和组合数性质,并能用它们解决一些简单的应用问题。
2、理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题。
1、掌握分类计数原理与分步计数原理、并能用它分析和解决一些简单的应用问题。
7、已知集合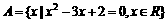 ,若
,若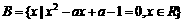 ,且
,且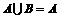 ,求实数a。
,求实数a。
解:∵A∪B=A,∴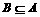 。
。
∵A={1,2},∴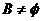 或B={1}或B={2}或B={1,2}。
或B={1}或B={2}或B={1,2}。
若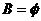 ,则由△<0知,不存在实数a使原方程有解;
,则由△<0知,不存在实数a使原方程有解;
若B={1},则由△=0得,a=2,此时1是方程的根;
若B={2},则由△=0得,a=2,此时2不是方程的根,
∴不存在实数a使原方程有解;
若B={1,2},则由△>0,得a∈R,且a≠2,
此时将x=1代入方程得a∈R,将x=2代入方程得a=3。
综上所述,实数a的值为2或3。
6、已知关于x的不等式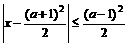 ,
,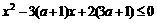 的解集依次为A、B,且
的解集依次为A、B,且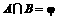 。求实数a的取值范围。
。求实数a的取值范围。
解: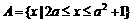 ,B={x|(x-2)[x-(3a+1)]≤0}
,B={x|(x-2)[x-(3a+1)]≤0}
∵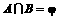
①当3a+1≥2时,B={x|2≤x≤3a+1}
∴3a+1<2a或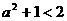 ,∴
,∴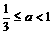
②当3a+1<2时,B={x|3a+1≤x≤2}
∴2a>2或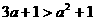 ,∴
,∴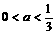
5、已知集合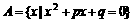 ,
,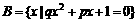 同时满足
同时满足
①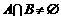 ,②
,②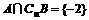 ,其中p、q均为不等于零的实数,求p、q的值。
,其中p、q均为不等于零的实数,求p、q的值。
解:条件①是说集合A、B有相同的元素,条件②是说-2∈A但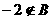 ,A、B是两个方程的解集,方程
,A、B是两个方程的解集,方程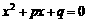 和
和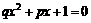 的根的关系的确定是该题的突破口。
的根的关系的确定是该题的突破口。
设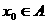 ,则
,则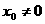 ,否则将有q=0与题设矛盾。于是由
,否则将有q=0与题设矛盾。于是由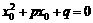 ,两边同除以
,两边同除以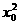 ,得
,得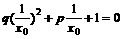 ,
,
知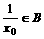 ,故集合A、B中的元素互为倒数。
,故集合A、B中的元素互为倒数。
由①知存在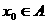 ,使得
,使得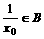 ,且
,且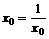 ,得
,得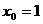 或
或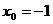 。
。
由②知A={1,-2}或A={-1,-2}。
若A={1,-2},则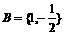 ,
,
有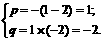
同理,若A={-1,-2},则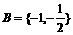 ,得p=3,q=2。
,得p=3,q=2。
综上,p=1,q=-2或p=3,q=2。
4、已知集合A=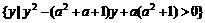 ,B=
,B=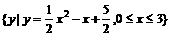 ;若
;若
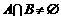 ,求实数a的取值范围。
,求实数a的取值范围。
解:B=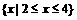 ,由
,由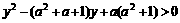 得:
得: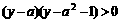
因为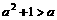 ,所以A=
,所以A=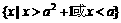 。
。
由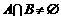 得:
得: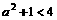 或
或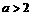
所以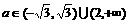
3、已知集合A=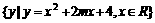 ,B=
,B=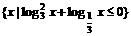 ,且
,且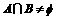 ,求实数
,求实数
m的值。
解: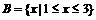 ,
,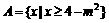 ,由
,由 得:
得: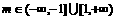
2、已知A=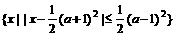 ,B=
,B=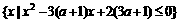 。若A
。若A B,求实数a的取值范围。
B,求实数a的取值范围。
解:易得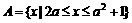 ,由
,由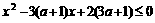 得
得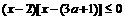
⑴当3a+1>2,即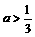 时,
时,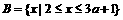
要使A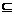 B,必须
B,必须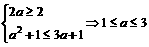 ,
,
⑵当3a+1=2,即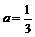 时,
时,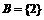 ;要使A
;要使A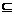 B,a=1
B,a=1
当3a+1<2,即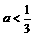 时,
时,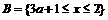
⑶要使A B,必须
B,必须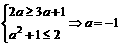
综上知: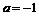 或
或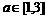
1、设A=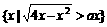 ,B=
,B=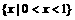 ;若A
;若A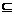 B,求实数a的取值范围。
B,求实数a的取值范围。
 解:由图象法解得:
解:由图象法解得:
当a>0时,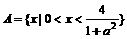 ;
;
当a≤0时,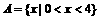
∴要使得A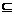 B,必须且只须
B,必须且只须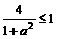 ,解得
,解得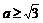
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com