
题目列表(包括答案和解析)
3.已知函数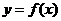 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当 (0,+∞)时,
(0,+∞)时,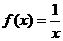 ,则当
,则当 (-∞,-2)时
(-∞,-2)时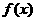 的解析式为( )
的解析式为( )
A. B.
B. C.
C.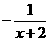 D.
D.
2.已知实数a,b均不为零,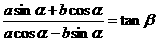 ,且
,且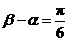 ,则
,则 等于( )
等于( )
A.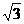 B.
B.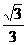 C.
C.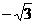 D.
D.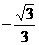
1.已知a>b>0,全集为R,集合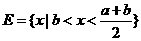 ,
,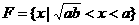 ,
,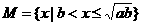 ,则有( )
,则有( )
A. (
(
 ) B.
) B.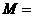 (
(
 )
)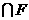
C.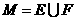 D.
D.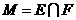
22.(14分)设函数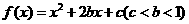 ,
,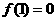 ,且方程
,且方程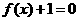 有实根.
有实根.
(1)证明:-3<c≤-1且b≥0;
(2)若m是方程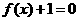 的一个实根,判断
的一个实根,判断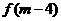 的正负并加以证明.
的正负并加以证明.
21.(12分)已知双曲线C: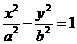 (a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足
(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足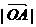 、
、 、
、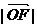 成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
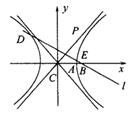
(1)求证: ;
;
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.
19.(12分)一个口袋中装有大小相同的2个白球和3个黑球.
(1)从中摸出两个球,求两球恰好颜色不同的概率;
(2)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率.
注意:考生在(20甲)、(20乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
20甲.(12分)如图,正三棱柱 的底面边长为a,点M在边BC上,△
的底面边长为a,点M在边BC上,△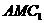 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
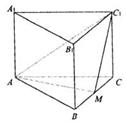
(1)求证点M为边BC的中点;
(2)求点C到平面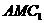 的距离;
的距离;
(3)求二面角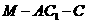 的大小.
的大小.
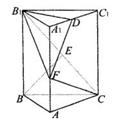
20乙.(12分)如图,直三棱柱 中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,
中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,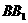 =3a,D为
=3a,D为 的中点,E为
的中点,E为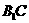 的中点.
的中点.
(1)求直线BE与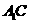 所成的角;
所成的角;
(2)在线段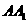 上是否存在点F,使CF⊥平面
上是否存在点F,使CF⊥平面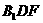 ,若存在,求出
,若存在,求出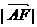 ;若不存在,说明理由.
;若不存在,说明理由.
18.(12分)已知等比数列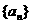 的公比为q,前n项的和为
的公比为q,前n项的和为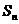 ,且
,且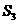 ,
,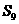 ,
,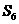 成等差数列.
成等差数列.
(1)求 的值;
的值;
(2)求证: ,
,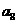 ,
,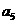 成等差数列.
成等差数列.
17.(12分)已知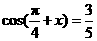 ,求
,求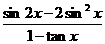 的值.
的值.
16.若对n个向量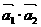 ,…,
,…,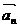 存在n个不全为零的实数
存在n个不全为零的实数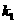 ,
,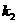 ,…,
,…, ,使得
,使得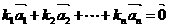 成立,则称向量
成立,则称向量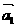 ,
,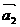 ,…,
,…,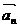 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明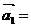 (1,2),
(1,2),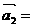 (1,-1),
(1,-1),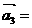 (2,2)“线性相关”的实数
(2,2)“线性相关”的实数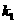 ,
,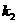 ,
,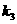 依次可以取________(写出一组数值即中,不必考虑所有情况).
依次可以取________(写出一组数值即中,不必考虑所有情况).
15.有A、B、C、D、E五名学生参加网页设计竞赛,决出了第一到第五的名次,A、B两位同学去问成绩,教师对A说:“你没能得第一名”.又对B说:“你得了第三名”.从这个问题分析,这五人的名次排列共有________种可能(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com