
题目列表(包括答案和解析)
5. 已知向量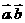 满足:
满足: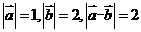 则
则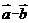 =
=
A 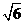 B
B
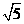 C
C
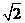 D.
1
D.
1
4. 不等式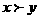 与
与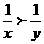 同时成立的充要条件是
同时成立的充要条件是
A 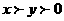 B
B
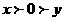 C
C 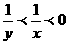 D
D 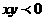
3.一个容量为20的样本数据,分组后,组距与频数如下;
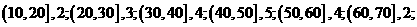 则样本
则样本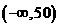 在上的频率为
在上的频率为
A 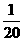 B
B
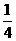 C
C 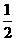 D
D
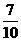
2. 已知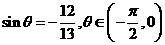 ,则
,则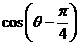 的值为
的值为
A. 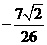 B
B 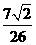 C
C
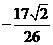 D
D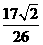
1. 已知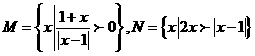 ,则
,则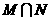 =
=
A. 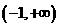 B
B
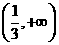
C 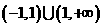 D
D
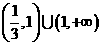
(17)(本小题满分12分)
某高级中学共有学生2000人,各年级男、女生人数如下表:
|
|
高一 |
高二 |
高三 |
|
女生 |
373 |
x |
y |
|
男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(Ⅰ)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少人?
(Ⅱ)已知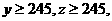 求高三年级女生比男生多的概率.
求高三年级女生比男生多的概率.
(18)(本小题满分12分)
已知 、
、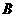 、
、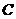 分别为
分别为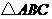 的三边
的三边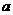 、
、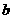 、
、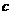 所对的角,向量
所对的角,向量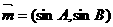 ,
,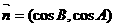 ,且
,且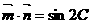 .
.
(Ⅰ)求角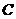 的大小;
的大小;
(Ⅱ)若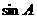 ,
,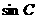 ,
,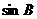 成等差数列,且
成等差数列,且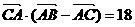 ,求边
,求边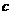 的长.
的长.
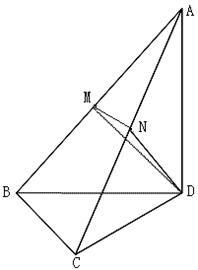
(19)(本小题满分12分)
如图,三棱锥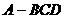 中,
中,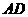 、
、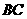 、
、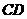 两两互相垂直,且
两两互相垂直,且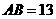 ,
,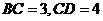 ,
,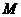 、
、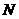 分别为
分别为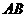 、
、 的中点.
的中点.
(Ⅰ)求证: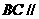 平面
平面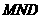 ;
;
(Ⅱ)求证:平面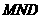
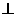 平面
平面 ;
;
(Ⅲ)求三棱锥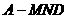 的体积.
的体积.
(20)(本小题满分12分)
已知等差数列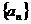 的前
的前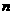 项和为
项和为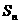 ,公差
,公差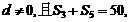
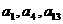 成等比数列.
成等比数列.
(Ⅰ)求数列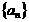 的通项公式;
的通项公式;
(Ⅱ)若从数列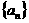 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……,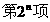 ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列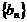 ,记该数列的前
,记该数列的前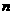 项和为
项和为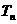 ,求
,求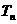 的表达式.
的表达式.
(21)(本小题满分12分)
已知定义在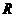 上的函数
上的函数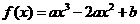
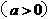 在区间
在区间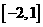 上的最大值是5,最小值是-11.
上的最大值是5,最小值是-11.
(Ⅰ)求函数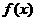 的解析式;
的解析式;
(Ⅱ)若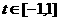 时,
时,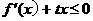 恒成立,求实数
恒成立,求实数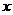 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知直线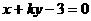 所经过的定点
所经过的定点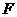 恰好是椭圆
恰好是椭圆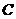 的一个焦点,且椭圆
的一个焦点,且椭圆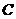 上的点到点
上的点到点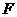 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆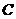 的标准方程;
的标准方程;
(Ⅱ)已知圆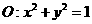 ,直线
,直线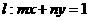 .试证明:当点
.试证明:当点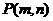 在椭圆
在椭圆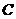 上运动时,直线
上运动时,直线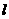 与圆
与圆 恒相交,并求直线
恒相交,并求直线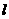 被圆
被圆 所截得弦长
所截得弦长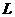 的取值范围.
的取值范围.
(13)若平面向量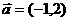 与
与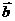 的夹角为180°,且
的夹角为180°,且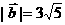 ,则
,则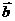 的坐标为
.
的坐标为
.
(14)在等差数列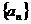 中,若
中,若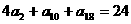 ,则数列
,则数列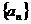 的前11项和
的前11项和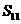 = .
= .
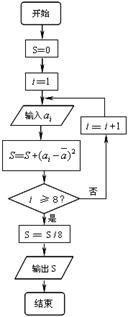 (15)对一个作直线运动的质点的运动过程观测了8次, 第
(15)对一个作直线运动的质点的运动过程观测了8次, 第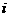 次观测
次观测
得到的数据为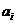 ,具体如下表所示:
,具体如下表所示:
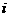 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
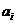 |
40 |
41 |
43 |
43 |
44 |
46 |
47 |
48 |
在对上述统计数据的分析中,一部分计算见如图所示的算法流程
图(其中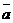 是这8个数据的平均数),则输出的
是这8个数据的平均数),则输出的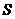 的值是_ .
的值是_ .
(16)如果直线y=kx+1与圆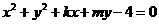 交于M、N
交于M、N
两点,且M、N关于直线x+y=0对称,若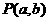 为平面区域
为平面区域
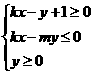 内任意一点,则
内任意一点,则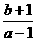 的取值范围是
.
的取值范围是
.
(1)集合A={-1,0,1},B={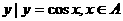 },则A
},则A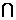 B=
B=
(A) {0} (B) {1} (C){0,1} (D){-1,0,1}
(2)已知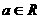 ,且
,且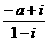 为实数,则
为实数,则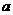 等于
等于
(A) 1
(B) 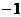 (C)
(C)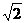 (D)
(D)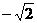
(3)使不等式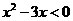 成立的必要不充分条件是
成立的必要不充分条件是
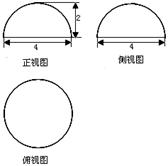 (A)
(A)
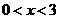 (B)
(B)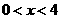
(C) 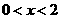 (D)
(D)
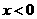 ,或
,或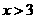
(4)右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积为
(A)32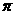 (B)16
(B)16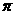
(C)12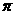 (D)8
(D)8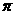
(5)偶函数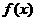 在区间[0,
在区间[0,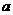 ](
](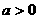 )上是单调函数,且
)上是单调函数,且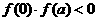 ,则方程
,则方程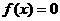 在区间[-
在区间[-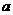 ,
,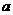 ]内根的个数是
]内根的个数是
(A) 3 (B) 2 (C) 1 (D)0
(6)在等比数列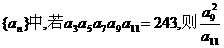 的值为
的值为
(A) 9 (B) 1 (C)2 (D)3
(7)在区域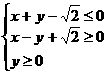 内任取一点
内任取一点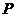 ,则点
,则点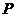 落在单位圆
落在单位圆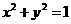 内的概率为
内的概率为
(A)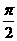 (B)
(B) 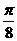 (C)
(C)
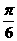 (D)
(D)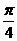
(8)以双曲线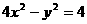 的中心为顶点,右焦点为焦点的抛物线方程是
的中心为顶点,右焦点为焦点的抛物线方程是
(A)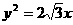 (B)
(B) 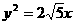 (C)
(C) 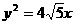 (D)
(D) 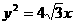
(9)已知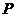 点在曲线
点在曲线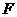 :
: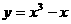 上,且曲线
上,且曲线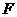 在点
在点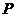 处的切线与直线
处的切线与直线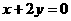 垂直,则点
垂直,则点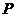 的坐标为
的坐标为
(A)(1,1) (B)(-1,0) (C)(-1,0)或(1,0) (D)(1,0)或(1,1)
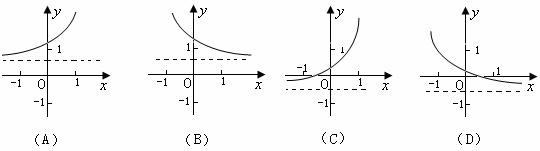
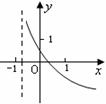 (10)已知函数
(10)已知函数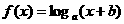 的大致图象如右图,其中
的大致图象如右图,其中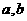 为常数,则
为常数,则
函数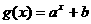 的大致图象是
的大致图象是
(11)定义运算: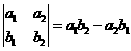 ,将函数
,将函数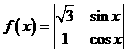 的图象向左平移
的图象向左平移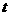 (
(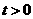 )个单位,所得图象对应的函数为偶函数,则
)个单位,所得图象对应的函数为偶函数,则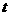 的最小值为
的最小值为
(A) 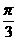 (B)
(B) 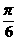 (C)
(C) 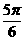 (D)
(D) 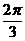
(12)下列结论
①命题“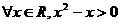 ”的否定是“
”的否定是“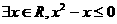 ”;
”;
②当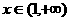 时,函数
时,函数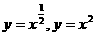 的图象都在直线
的图象都在直线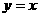 的上方;
的上方;
③定义在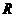 上的奇函数
上的奇函数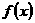 ,满足
,满足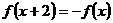 ,则
,则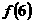 的值为0.
的值为0.
④若函数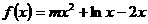 在定义域内是增函数,则实数
在定义域内是增函数,则实数 的取值范围为
的取值范围为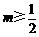 .
.
其中,正确结论的个数是
(A) 1 (B) 2 (C) 3 (D) 4
第Ⅱ卷(非选择题 共90分)
⒈ 第Ⅱ卷包括填空题和解答题共两个大题.
⒉ 第Ⅱ卷所有题目的答案,使用0.5毫米的黑色中性(签字)笔书写,字体工整,笔迹清楚.
⒊ 请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
22.B(本小题满分10分)选修4-4:坐标系与参数方程
已知圆系的方程为x2+y2-2axCos -2aySin
-2aySin =0(a>0)
=0(a>0)
(1)求圆系圆心的轨迹方程;
(2)证明圆心轨迹与动圆相交所得的公共弦长为定值;
22.A.(本小题满分10分)选修4-1:几何证明选讲
如图所示,已知⊙O1与⊙O2相交于A,B两点,过
 点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割
点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割
线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于
点P.
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com