
题目列表(包括答案和解析)
6.设F1,F2分别是双曲线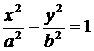 的左右焦点,若双曲线上存在点A,使∠F1AF2=90°且|AF1|=3|AF2|,则双曲线的离心率等于 ( )
的左右焦点,若双曲线上存在点A,使∠F1AF2=90°且|AF1|=3|AF2|,则双曲线的离心率等于 ( )
A.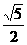 B.
B.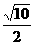 C.
C.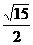 D.
D.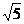
5.点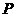 在直线
在直线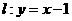 上,若存在过
上,若存在过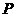 的直线交抛物线
的直线交抛物线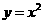 于
于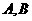 两点,且
两点,且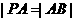 ,则称点
,则称点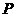 为“点”,那么下列结论中正确的是
为“点”,那么下列结论中正确的是
A.直线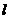 上的所有点都是“
上的所有点都是“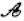 点” B.直线
点” B.直线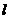 上仅有有限个点是“
上仅有有限个点是“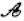 点”
点”
C.直线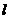 上的所有点都不是“
上的所有点都不是“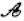 点” D.直线
点” D.直线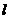 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“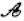 点”
点”
4.设抛物线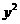 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(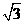 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,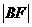 =2,则
=2,则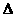 BCF与
BCF与 ACF的成面积之比
ACF的成面积之比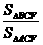 =
=
A.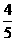 B.
B.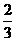 C.
C.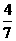 D.
D.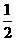 w
w
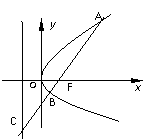
3.如图,过抛物线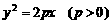 的焦点F的直线
的焦点F的直线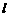 交抛物线于点A.B,交其准线于点C,若
交抛物线于点A.B,交其准线于点C,若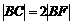 ,且
,且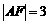 ,则此抛物线的方程为
( )
,则此抛物线的方程为
( )
 A.
A.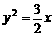 B.
B.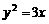
C.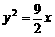 D.
D.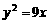
2.若抛物线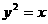 上一点
上一点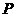 到准线的距离等于它到顶点的距离,则点
到准线的距离等于它到顶点的距离,则点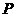 的坐标为( )
的坐标为( )
A.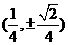 B.
B.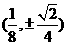 C.
C.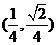 D.
D.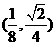
1.设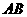 为过抛物线
为过抛物线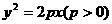 的焦点的弦,则
的焦点的弦,则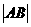 的最小值为( )
的最小值为( )
A.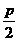 B.
B.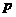 C.
C.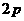 D.无法确定
D.无法确定
17. 已知平行六面体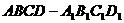 的底面为正方形,
的底面为正方形,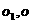 分别为上、下底面的中心,且
分别为上、下底面的中心,且 在底面
在底面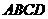 的射影是
的射影是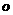 。
。
 (I)求证:平面
(I)求证:平面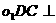 平面
平面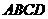
(II)若点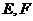 分别在棱上
分别在棱上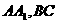 上,且
上,且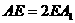 ,问点
,问点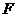 在何处时,
在何处时,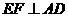
(III)若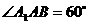 ,求二面角
,求二面角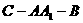 的大小(用反三角函数表示)
的大小(用反三角函数表示)
16.  如图,斜三棱柱
如图,斜三棱柱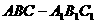 ,已知侧面
,已知侧面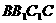 与底面ABC垂直且∠BCA=90°,∠
与底面ABC垂直且∠BCA=90°,∠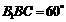 ,
,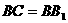 =2,若二面角
=2,若二面角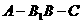 为30°,
为30°,
(Ⅰ)证明 ;
;
(Ⅱ)求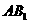 与平面
与平面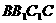 所成角的正切值;
所成角的正切值;
(Ⅲ)在平面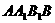 内找一点P,使三棱锥
内找一点P,使三棱锥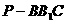 为正三棱锥,并求P到平面
为正三棱锥,并求P到平面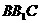 距离
距离
15.如图所示,已知直三棱柱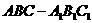 中,
中, =90o,侧面
=90o,侧面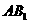 与侧面
与侧面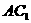 所成的二面角为60°,M为
所成的二面角为60°,M为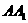 上的点,
上的点,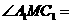 30°,
30°,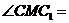 90°,
90°,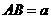 .
.
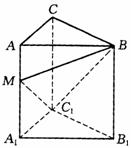
(1)求BM与侧面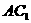 所成角的正切值;
所成角的正切值;
(2)求顶点A到面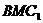 的距离.
的距离.
14.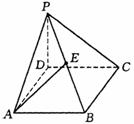 如图所示,PD垂直于正方形ABCD所在平面,AB=2,E是PB的中点,
如图所示,PD垂直于正方形ABCD所在平面,AB=2,E是PB的中点,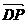 与
与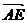 夹角的余弦值为
夹角的余弦值为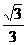

(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF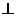 平面PCB.
平面PCB.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com