
题目列表(包括答案和解析)
17. 已知抛物线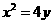 ,过定点
,过定点 的直线
的直线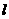 交抛物线于A、B两点.
交抛物线于A、B两点.
(Ⅰ)分别过A、B作抛物线的两条切线,A、B为切点,求证:这两条切线的交点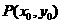 在定直线
在定直线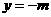 上.
上.
(Ⅱ)当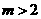 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线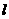 对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用
对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.
16.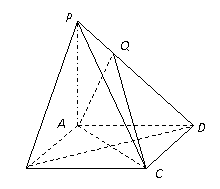 如图,棱锥
如图,棱锥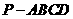 的底面
的底面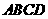 是矩形,
是矩形,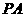 ⊥平面
⊥平面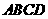 ,
,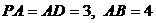 ,
,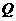 为棱
为棱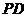 上一点,且
上一点,且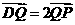 .
.
(Ⅰ)求二面角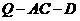 的余弦值;
的余弦值;
(Ⅱ)求点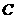 到平面
到平面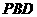 的距离.
的距离.
15. 已知向量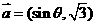 ,
,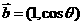 ,
,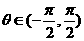 .
.
(1)若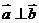 ,求
,求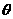 ;(2)求
;(2)求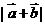 的最大值.
的最大值.
19. 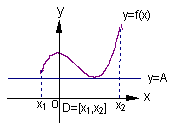 如右图(1)所示,定义在区间
如右图(1)所示,定义在区间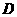 上的函数
上的函数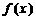 ,如果满
,如果满
足:对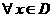 ,
,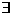 常数A,都有
常数A,都有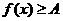 成立,则称函数
成立,则称函数
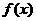 在区间
在区间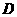 上有下界,其中
上有下界,其中 称为函数的下界. (提示:图(1)、
称为函数的下界. (提示:图(1)、
(2)中的常数 、
、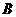 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
(Ⅰ)试判断函数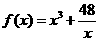 在
在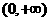 上是否有下界?并说明理由;
上是否有下界?并说明理由;
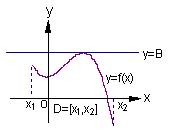 (Ⅱ)又如具有右图(2)特征的函数称为在区间
(Ⅱ)又如具有右图(2)特征的函数称为在区间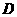 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数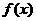 在区间
在区间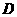 上
上
有上界的定义,并判断(Ⅰ)中的函数在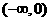 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数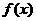 在区间
在区间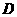 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数
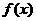 在区间
在区间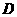 上有界,函数
上有界,函数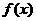 叫做有界函数.试探究函数
叫做有界函数.试探究函数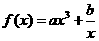 (
(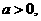
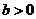
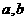 是常数)是否是
是常数)是否是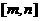 (
(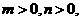
 、
、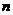 是常数)上的有
是常数)上的有
18. 已知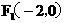 ,
,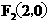 ,点
,点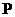 满足
满足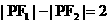 ,记点
,记点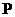 的轨迹为
的轨迹为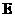 ,直线
,直线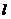 过点
过点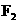 且与轨迹
且与轨迹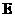 交于
交于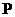 、
、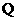 两点.
两点.
(1)无论直线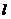 绕点
绕点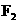 怎样转动,在
怎样转动,在 轴上总存在定点
轴上总存在定点 ,使
,使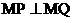 恒成立,求实数
恒成立,求实数 的值.
的值.
(2)过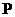 、
、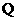 作直线
作直线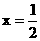 的垂线
的垂线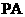 、
、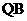 ,垂足分别为
,垂足分别为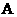 、
、 ,记
,记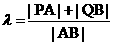 ,求
,求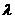 的取值范围.
的取值范围.
17. 设数列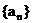 的各项都是正数, 且对任意
的各项都是正数, 且对任意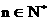 都有
都有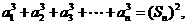 记
记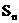 为数列
为数列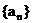 的前n项和.
的前n项和.
(1) 求证: 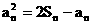 ;(2) 求数列
;(2) 求数列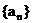 的通项公式;
的通项公式;
(3) 若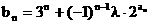 (
(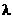 为非零常数,
为非零常数, 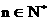 ), 问是否存在整数
), 问是否存在整数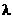 , 使得对任意
, 使得对任意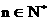 ,
,
都有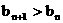 .
.
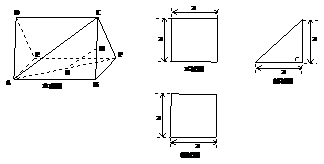
16. .如图,多面体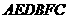 的直观图及三视图如图所示,
的直观图及三视图如图所示,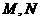 分别
分别
 为
为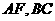 的中点.
的中点.
(1)求证: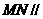 平面
平面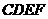 ;
;
(2)求多面体 的体积;
的体积;
(3)求证: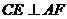 .
.
15.已知向量: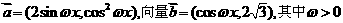 ,设函数
,设函数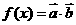 ,若
,若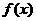 图象的相邻两对称轴间的距离为
图象的相邻两对称轴间的距离为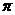 .
.
(Ⅰ)求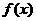 的解析式;
的解析式;
(Ⅱ)若对任意实数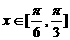 ,恒有
,恒有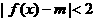 成立,求实数
成立,求实数 的取值范围.
的取值范围.
14.在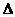 ABC中,
ABC中,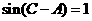 , sinB=
, sinB=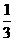 . sinA=_____;
. sinA=_____;
广东省惠州市10届艺术类考生数学复习小节训练卷(22)
13.设△ABC的内角A、B、C的对边长分别为a、b、c,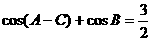 ,
,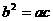 ,B=_______.
,B=_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com