
题目列表(包括答案和解析)
4个选项中,只有一项是符合题目要求的.
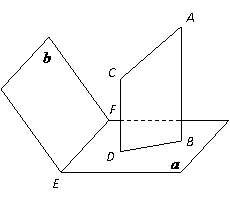
(1)复数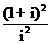 等于
等于
(A)2
(B)-2
(C)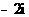 (D)
(D)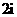
(2)命题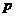 :
: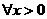 ,都有
,都有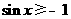 ,则
,则
(A)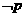 :
: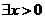 ,使得
,使得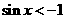 (B)
(B)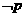 :
: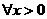 ,都有
,都有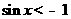
(C)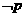 :
: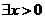 ,使得
,使得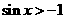 (D)
(D)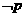 :
: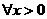 ,都有
,都有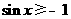
(3)满足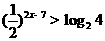 成立的
成立的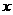 的取值范围是
的取值范围是
(A)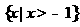 (B)
(B)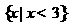
(C)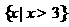 (D)
(D)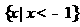
(4)下列函数中,最小正周期为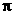 ,且图象关于直线
,且图象关于直线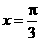 对称的是
对称的是
(A)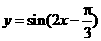 (B)
(B)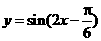
(C)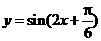 (D)
(D)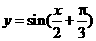
(5)一只小蜜蜂在一个棱长为30的正方体玻璃容器内随机飞行,若蜜蜂在飞行过程中与正方体玻璃容器6个表面中至少有一个的距离不大于10,则就有可能撞到玻璃上而不安全;若始终保持与正方体玻璃容器6个表面的距离均大于10,则飞行是安全的,假设蜜蜂在正方体玻璃容器内飞行到每一位置可能性相同,那么蜜蜂飞行是安全的概率是
(A) 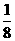 (B)
(B) 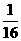 (C)
(C) 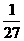 (D)
(D) 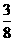
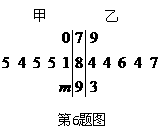
(6)右图是某年青年歌手大奖赛中,七位评委为甲乙两名选手打出的分数的茎叶图(其中m为数字0-9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有
(A)a1>a2 (B)a1<a2
(C)a1=a2 (D)a1,a2的大小与m的值有关
(7)设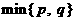 表示
表示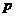 ,
,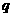 两者中的较小者,若函数
两者中的较小者,若函数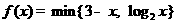 ,则满足
,则满足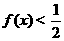 的
的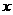 的集合为
的集合为
(A)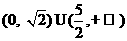 (B)
(B)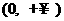
(C)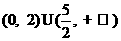 (D)
(D)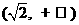
 (8)如图,设平面
(8)如图,设平面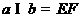 ,
,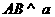 ,
,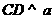 ,垂足分别为
,垂足分别为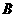 ,
,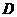 ,且
,且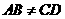 .如果增加一个条件就能推出
.如果增加一个条件就能推出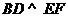 ,给出四个条件:①
,给出四个条件:①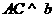 ;②
;②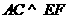 ;③
;③ 与
与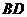 在
在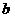 内的正投影在同一条直线上 ;④
内的正投影在同一条直线上 ;④ 与
与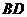 在平面
在平面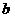 内的正投影所在的直线交于一点. 那么这个条件不可能是
内的正投影所在的直线交于一点. 那么这个条件不可能是
(A)①② (B)②③
(C)③ (D)④
第II卷(非选择题 共110分)
(15)(本小题共12分)
在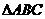 中,角
中,角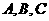 所对的边分别为
所对的边分别为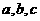 ,满足
,满足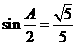 ,且
,且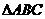 的面积为
的面积为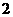 .
.
(Ⅰ)求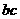 的值;
的值;
(Ⅱ)若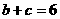 ,求
,求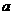 的值.
的值.
(16)(本小题共13分)
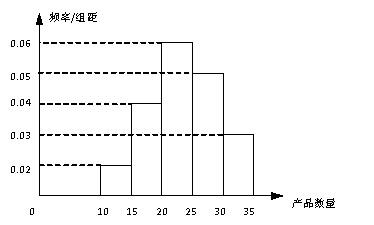
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为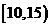 ,
,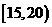 ,
,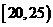 ,
,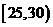 ,
,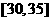 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在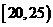 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
 (Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?
(Ⅱ)工厂规定从各组中任选1人进行再培训,则选取5人的概率是多少?
(17)(本小题共14分)
 三棱柱
三棱柱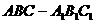 中,侧棱与底面垂直,
中,侧棱与底面垂直,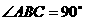 ,
,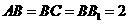 ,
, 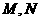 分别是
分别是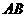 ,
,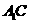 的中点.
的中点.
(Ⅰ)求证: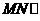 平面
平面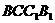 ;
;
(Ⅱ)求证: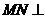 平面
平面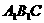 ;
;
(Ⅲ)求二面角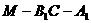 的余弦值.
的余弦值.
(18)(本小题共14分)
已知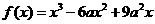 (
( ).
).
(Ⅰ)求函数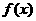 的单调递减区间;
的单调递减区间;
(Ⅱ)当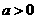 时,若对
时,若对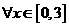 有
有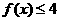 恒成立,求实数
恒成立,求实数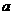 的取值范围.
的取值范围.
(19)(本小题共14分)
已知抛物线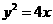 ,点
,点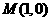 关于
关于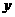 轴的对称点为
轴的对称点为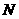 ,直线
,直线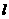 过点
过点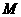 交抛物线于
交抛物线于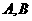 两点.
两点.
(Ⅰ)证明:直线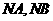 的斜率互为相反数;
的斜率互为相反数;
(Ⅱ)求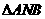 面积的最小值;
面积的最小值;
(Ⅲ)当点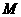 的坐标为
的坐标为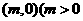 ,且
,且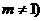 .根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
.根据(Ⅰ)(Ⅱ)推测并回答下列问题(不必说明理由):
① 直线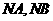 的斜率是否互为相反数?
的斜率是否互为相反数?
② 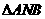 面积的最小值是多少?
面积的最小值是多少?
(20)(本小题共13分)
已知数列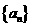 中,
中,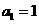 ,
,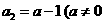 且
且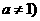 ,其前
,其前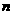 项和为
项和为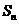 ,且当
,且当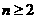 时,
时,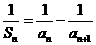 .
.
(Ⅰ)求证:数列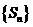 是等比数列;
是等比数列;
(Ⅱ)求数列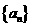 的通项公式;
的通项公式;
(Ⅲ)若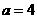 ,令
,令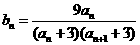 ,记数列
,记数列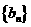 的前
的前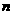 项和为
项和为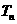 .设
.设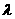 是整数,问是否存在正整数
是整数,问是否存在正整数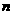 ,使等式
,使等式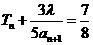 成立?若存在,求出
成立?若存在,求出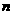 和相应的
和相应的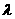 值;若不存在,请说明理由.
值;若不存在,请说明理由.
gaokao/beijing/
崇文区2009-2010学年度第二学期统一练习(一)
(9)如果复数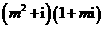 (其中
(其中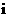 是虚数单位)是实数,则实数
是虚数单位)是实数,则实数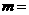 ___________.
___________.
(10)若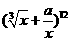 的展开式中的常数项为
的展开式中的常数项为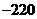 ,则实数
,则实数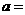 ___________.
___________.
(11)将参数方程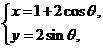 (
(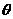 为参数)化成普通方程为 .
为参数)化成普通方程为 .
 (12)某程序框图如图所示,该程序运行后输出
(12)某程序框图如图所示,该程序运行后输出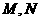 的值分别为
.
的值分别为
.
(13)若数列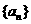 的前
的前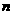 项和为
项和为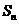 ,则
,则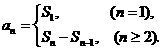
若数列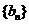 的前
的前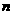 项积为
项积为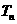 ,类比上述结果,则
,类比上述结果,则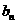 =_________;
=_________;
此时,若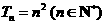 ,则
,则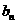 =___________.
=___________.
(14)定义在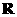 上的函数满足
上的函数满足 ,
,
且当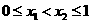 时,
时,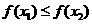 ,则
,则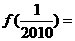 _________________.
_________________.
(1)已知全集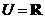 ,集合
,集合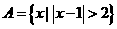 ,
,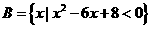 ,则集合
,则集合
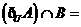
(A)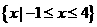 (B)
(B)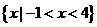
(C)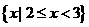 (D)
(D) 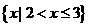
(2)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人. 为了调查职工的健康状况,用分层抽样的方法从全体职工中抽出一个容量为25的样本,应抽取不超过45岁的职工人数为
 (A)
5
(B) 10 (C)15 (D)50
(A)
5
(B) 10 (C)15 (D)50
(3)已知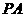 是
是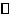
 的切线,切点为
的切线,切点为 ,
,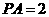 ,
, 是
是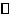

的直径,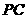 交
交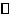
 于点
于点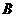 ,
,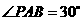 ,则
,则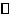
 的
的
半径为
(A)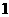 (B)
(B)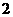
(C)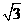 (D)
(D)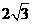
(4)已知等比数列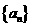 为递增数列,且
为递增数列,且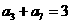 ,
,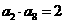 ,则
,则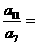
(A)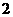 (B)
(B)
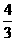 (C)
(C) 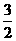 (D)
(D)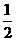
(5)已知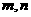 是两条不同直线,
是两条不同直线,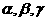 是三个不同平面,下列命题中正确的为
是三个不同平面,下列命题中正确的为
(A)若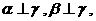 则
则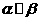 (B)若
(B)若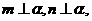 则
则
(C)若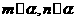 ,则
,则 (D)若
(D)若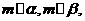 则
则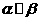
(6)设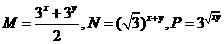 (其中
(其中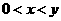 ), 则
), 则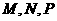 大小关系为
大小关系为
(A)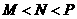 (B)
(B)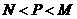 (C)
(C)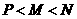 (D)
(D)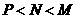
(7)2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为
(A)36 (B)42 (C) 48 (D) 60
(8)设定义在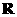 上的函数
上的函数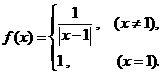 若关于
若关于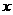 的方程
的方程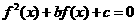 有3个不同的实数解
有3个不同的实数解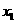 ,
,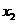 ,
,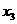 ,则
,则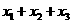 等于
等于
(A) 3 (B)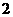 (C)
(C)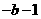 (D)
(D)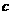
gaokao/beijing/
第Ⅱ卷(共110分)
20.(14分)
设集合W由满足下列两个条件的数列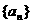 构成:
构成:
①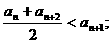
②存在实数M,使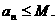 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列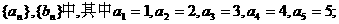
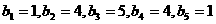 ;试判断数列
;试判断数列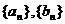 是否为集合W的元素;
是否为集合W的元素;
(II)设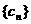 是各项为正的等比数列,
是各项为正的等比数列,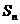 是其前n项和,
是其前n项和,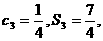 证明数列
证明数列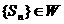 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列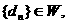 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有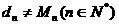 .
.
求证:数列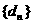 单调递增.
单调递增.
19.(13分)
在直角坐标系 中,点M到点
中,点M到点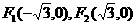 的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线
的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线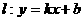 与轨迹C交于不同的两点P和Q.
与轨迹C交于不同的两点P和Q.
(I)求轨迹C的方程;
(II)当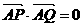 时,求k与b的关系,并证明直线
时,求k与b的关系,并证明直线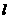 过定点.
过定点.
18.(13分)www..co
已知函数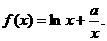
(I)当a<0时,求函数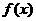 的单调区间;
的单调区间;
(II)若函数f(x)在[1,e]上的最小值是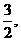 求a的值.
求a的值.
17.(14分)
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为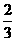 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为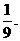
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为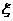 ,求
,求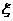 的分布列与均值E
的分布列与均值E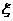 .
.
16.(13分)
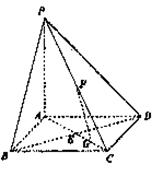
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(I)求证:BD⊥FG;
(II)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
 (III)当二面角B-PC-D的大小为
(III)当二面角B-PC-D的大小为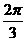 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
演算步骤或证明过程.
15.(12分)
已知函数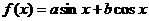 的图象经过点
的图象经过点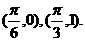
(I)求实数a、b的值;
(II)若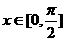 ,求函数
,求函数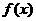 的最大值及此时x的值.
的最大值及此时x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com