
题目列表(包括答案和解析)
3. 德阳二模
2. 日照一模
(20)(本小题满分12分)
已知数列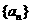 的前
的前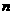 项和为
项和为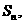 且
且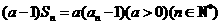 。
。
(Ⅰ)求证数列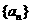 是等比数列,并求
是等比数列,并求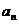 ;
;
(Ⅱ)已知集合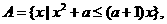 问是否存在实数
问是否存在实数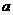 ,使得对于任意的
,使得对于任意的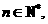 都有
都有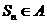 ?若存在,求出
?若存在,求出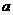 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(20)解:(Ⅰ)当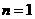 时,
时, 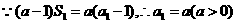 …………………………1分
…………………………1分
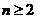 时,由
时,由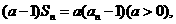 得
得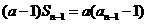
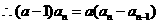 ,变形得:
,变形得: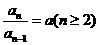 ………………………………………4分
………………………………………4分
故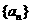 是以
是以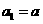 为首项,公比为
为首项,公比为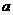 的等比数列,
的等比数列,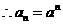 ………………………………6分
………………………………6分
(Ⅱ)(1)当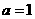 时,
时,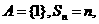 只有
只有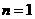 时
时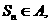
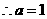 不适合题意
……………………………………………………7分
不适合题意
……………………………………………………7分
(2)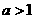 时,
时,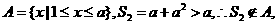
即当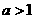 时,不存在满足条件的实数
时,不存在满足条件的实数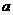 ………………………………………………………9分
………………………………………………………9分
(3)当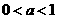 时,
时,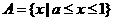
而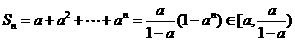
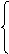 因此对任意的
因此对任意的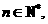 要使
要使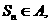 只需
只需 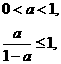 解得
解得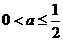 ………………………11分
………………………11分
综上得实数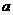 的范围是
的范围是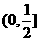 ……………………………………………………12分
……………………………………………………12分
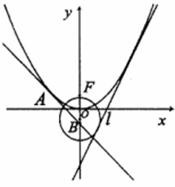 (21)(本小题满分12分)
(21)(本小题满分12分)
已知抛物线 的方程是
的方程是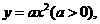 圆
圆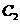 的方程是
的方程是
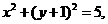 直线
直线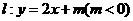 是
是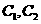 的公切
的公切
线, 是
是 的焦点.
的焦点.
(Ⅰ)求 与
与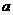 的值;
的值;
(Ⅱ)设 是抛物线
是抛物线 上的一动点,以
上的一动点,以 为切点作
为切点作 的
的
切线交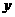 轴于点
轴于点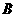 ,若
,若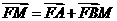 ,则点
,则点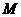 在一定直线上,试证明之。
在一定直线上,试证明之。
(21)解:(Ⅰ)由己知,圆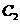 的圆心为
的圆心为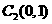 ,半径
,半径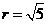
由题设圆心到直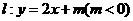 的距离
的距离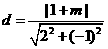
即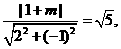 解得
解得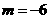 (
(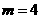 舍去)…………………………………………3分
舍去)…………………………………………3分
设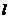 与抛物线相切的切点为
与抛物线相切的切点为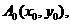 又
又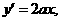 得
得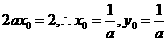
代入直线方程,得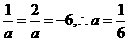 ……………………6分
……………………6分
所以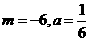
(Ⅱ)由(Ⅰ)知抛物线 的方程为
的方程为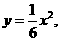 焦点
焦点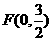
设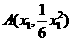 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线方程为
为切点的切线方程为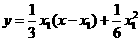 …………8分
…………8分
令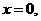 得点
得点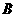 的坐标为
的坐标为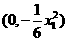
所以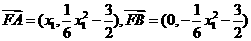 ……………………………………………10分
……………………………………………10分
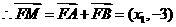 ,因
,因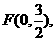 设
设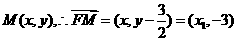
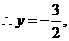 即
即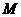 点在定直线
点在定直线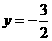 上 ……………………………………………………12分
上 ……………………………………………………12分
(22)(本小题满分14分)
己知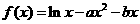 。
。
(Ⅰ)若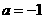 ,函数
,函数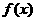 在其定义域内是增函数,求
在其定义域内是增函数,求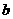 的取值范围;
的取值范围;
(Ⅱ)当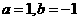 时,证明函数
时,证明函数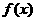 只有一个零点;
只有一个零点;
(Ⅲ)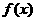 的图象与
的图象与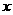 轴交于
轴交于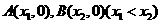 两点
两点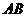 中点为
中点为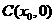 ,求证:
,求证: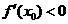 。
。
(22)解:(Ⅰ)依题意: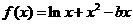
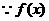 在
在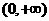 上递增,
上递增,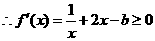 对
对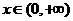 恒成立
恒成立
即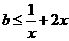 对
对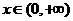 恒成立,
恒成立, 只需
只需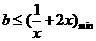 ……………………………2分
……………………………2分
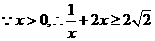 当且仅当
当且仅当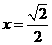 时取
时取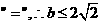 ,
,
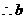 的取值范围为
的取值范围为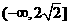 ……………………………………………………………4分
……………………………………………………………4分
(Ⅱ)当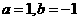 时,
时,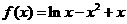 ,其定义域是
,其定义域是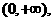
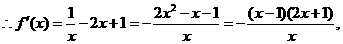 ……………………………………6分
……………………………………6分
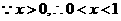 时,
时,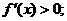 当
当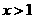 时,
时,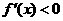
 函数
函数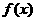 在区间
在区间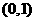 上单调递增,在区间
上单调递增,在区间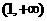 上单调递减
上单调递减
 当
当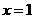 时,函数
时,函数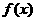 取得最大值,其值为
取得最大值,其值为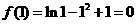
当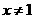 时,
时,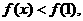 即
即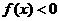
 函数
函数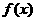 只有一个零点 ……………………………………………………………9分
只有一个零点 ……………………………………………………………9分
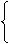
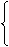 (Ⅲ)由已知得
(Ⅲ)由已知得
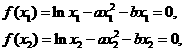
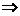
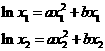 两式相减,得
两式相减,得
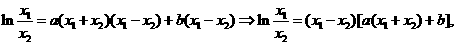 …………11分
…………11分
由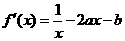 及
及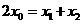 ,得
,得
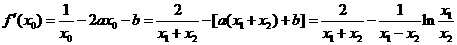
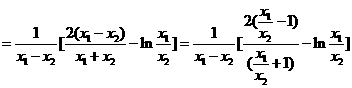 …………………………………12分
…………………………………12分
令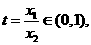 且
且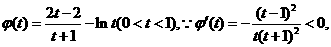
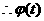 在
在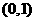 上递减,
上递减,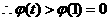
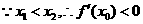 ……………………………………………………………………14分
……………………………………………………………………14分
19.(本小题满分12分)
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①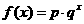 ;②
;②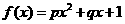 ;③
;③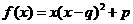 .(以上三式中、均为常数,且
.(以上三式中、均为常数,且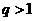 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(II)若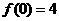 ,
,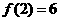 ,求出所选函数
,求出所选函数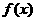 的解析式(注:函数定义域是
的解析式(注:函数定义域是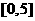 .其中
.其中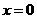 表示8月1日,
表示8月1日,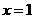 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
解:(I)根据题意,应选模拟函数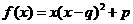 2分
2分
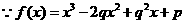 ,
,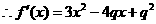 3分
3分
 若
若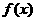 ≥
≥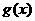 恒成立,即
恒成立,即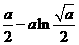 ≥
≥ 恒成立
恒成立
解之得≤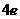 .
10分
.
10分
(III)由(II)得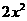 ≥
≥ ,即
,即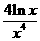 ≤
≤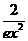 11分
11分
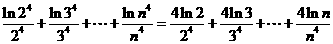
≤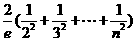
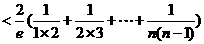 12分
12分
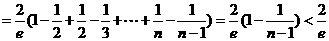 13分
13分
 所以
所以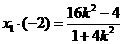 ,得
,得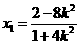 9分
9分
所以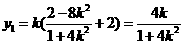
所以直线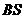 的斜率为
的斜率为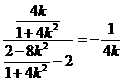 ,
10分
,
10分
则直线 的方程可设为
的方程可设为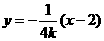
由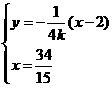 ,得
,得 点的坐标为
点的坐标为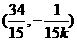 12分
12分
所以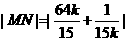 ≥
≥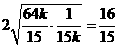
当且仅当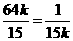 即
即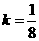 时取等号.
14分
时取等号.
14分
1.宁乡县开模
20.证明:
假设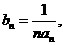 ∴
∴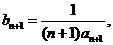 ………1分
………1分
∵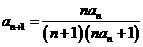 ,
,
∴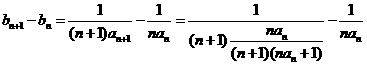 =
=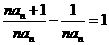
…………………………………3分

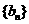 是首项为2,公差为1的等差数列.
………………………………4分
是首项为2,公差为1的等差数列.
………………………………4分

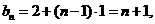
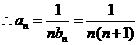 =
=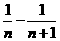 , …………6分
, …………6分
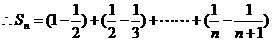 =
=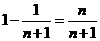 . …………8分
. …………8分
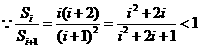 , …………………………………9分
, …………………………………9分
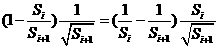
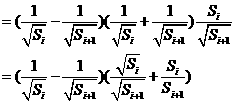
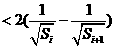 . …………………………………13分
. …………………………………13分

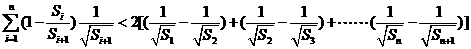
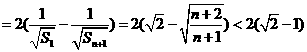 .…………16
.…………16
20. (本小题满分16分)数列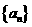 中,
中,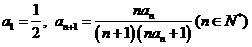 ,其前
,其前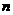 项的和为
项的和为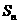 .求证:
.求证: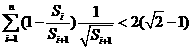 .
.
19.解: 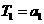 ,对
,对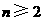 反复使用上述关系式,得
反复使用上述关系式,得
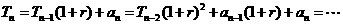
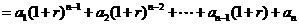 , ①
, ①
在①式两端同乘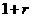 ,得
,得
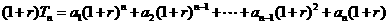 ②
②
②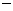 ①,得
①,得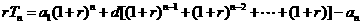
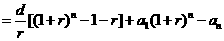 .
.
即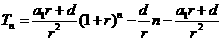 .
.
如果记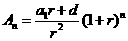 ,
,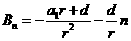 ,
,
则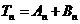 .
.
其中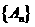 是以
是以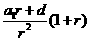 为首项,以
为首项,以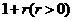 为公比的等比数列;
为公比的等比数列;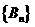 是以
是以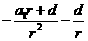 为首项,
为首项,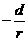 为公差的等差数列.
为公差的等差数列.
19.(本小题满分16分)
公民在就业的第一年就交纳养老储备金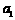 ,以后每年交纳的数目均比上一年增加
,以后每年交纳的数目均比上一年增加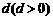 ,历年所交纳的储备金数目
,历年所交纳的储备金数目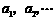 是一个公差为
是一个公差为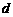 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为
的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.如果固定年利率为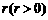 ,那么,在第
,那么,在第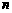 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为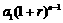 ,第二年所交纳的储备金就变为
,第二年所交纳的储备金就变为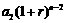 ,
, .以
.以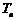 表示到第
表示到第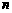 年末所累计的储备金总额.
年末所累计的储备金总额.
求证: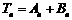 ,其中
,其中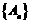 是一个等比数列,
是一个等比数列,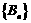 是一个等差数列.
是一个等差数列.
18.解:(I)证明:首先,由 中元素构成的有序数对
中元素构成的有序数对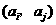 共有
共有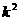 个.
个.
因为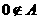 ,所以
,所以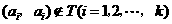 ;
;
又因为当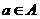 时,
时,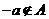 时,
时,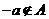 ,所以当
,所以当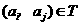 时,
时,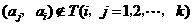 .
.
从而,集合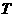 中元素的个数最多为
中元素的个数最多为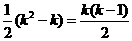 ,
,
即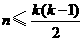 .
.
(II)解: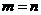 ,证明如下:
,证明如下:
(1)对于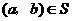 ,根据定义,
,根据定义,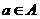 ,
, ,且
,且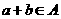 ,从而
,从而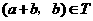 .
.
如果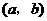 与
与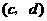 是
是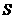 的不同元素,那么
的不同元素,那么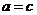 与
与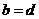 中至少有一个不成立,从而
中至少有一个不成立,从而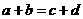 与
与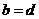 中也至少有一个不成立.
中也至少有一个不成立.
故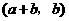 与
与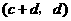 也是
也是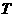 的不同元素.
的不同元素.
可见,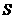 中元素的个数不多于
中元素的个数不多于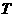 中元素的个数,即
中元素的个数,即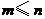 ,
,
(2)对于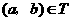 ,根据定义,
,根据定义,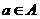 ,
, ,且
,且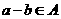 ,从而
,从而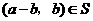 .如果
.如果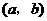 与
与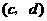 是
是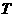 的不同元素,那么
的不同元素,那么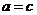 与
与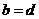 中至少有一个不成立,从而
中至少有一个不成立,从而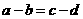 与
与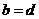 中也不至少有一个不成立,
中也不至少有一个不成立,
故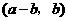 与
与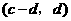 也是
也是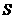 的不同元素.
的不同元素.
可见,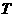 中元素的个数不多于
中元素的个数不多于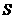 中元素的个数,即
中元素的个数,即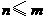 ,
,
由(1)(2)可知,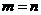 .
.
18. (本小题满分14分)
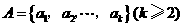 ,其中
,其中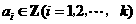 ,由
,由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: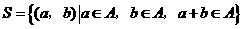 ,
,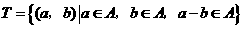 .其中
.其中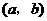 是有序数对,集合
是有序数对,集合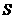 和
和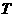 中的元素个数分别为
中的元素个数分别为 和
和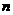 .若对于任意的
.若对于任意的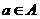 ,总有
,总有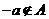 ,则称集合
,则称集合 具有性质
具有性质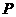 .
.
(I)对任何具有性质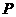 的集合
的集合 ,证明:
,证明: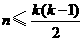 ;
;
(II)判断 和
和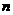 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com