
题目列表(包括答案和解析)
24.(本题满分10分)
证明:下面用数学归纳法证明
(1)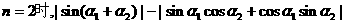
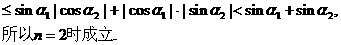
(2)假设 时成立,即
时成立,即
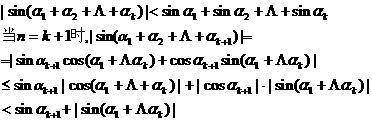

由(1)(2)得,原式成立。 ………………10分
23.(本题满分10分)
(I)直线的普通方程为: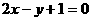 ;
;
圆的直角坐标方程为: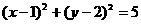 ………………4分
………………4分
(II)圆心到直线的距离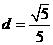 ,
,
直线被圆截得的弦长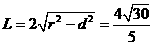 ………………10分
………………10分
22.(本题满分10分)
(I)证明:

∴圆心O在直线AD上。 ………………5分
(II)连接DF,由(I)知,DH是⊙O的直径,

∴点C是线段GD的中点。 ………………10分
22.(本小题满分10分)选修4-1:几何证明选讲
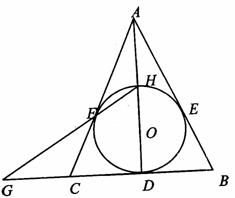 如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(I)求证:圆心O在直线AD上;
(II)求证:点C是线段GD的中点。
21.(本题满分12分)
解:(I)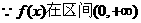 上是单调增函数,
上是单调增函数,
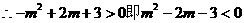
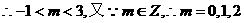 ………………2分
………………2分
而 是偶函数。
是偶函数。
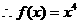 ………………4分
………………4分
(II)(i)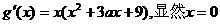 不是方程
不是方程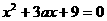 的根。
的根。
为使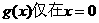 处有极值,
处有极值,
必须 恒成立, ………………6分
恒成立, ………………6分
即有
得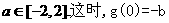 是唯一极值。
是唯一极值。
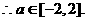 ………………8分
………………8分
(ii)由条件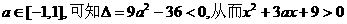 恒成立。
恒成立。
当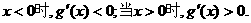 ………………9分
………………9分
因此函数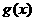 在[-2,2]上的最大值是
在[-2,2]上的最大值是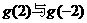 两者中较大者。 …………10分
两者中较大者。 …………10分
为使对方任意的 ,不等式
,不等式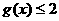 在[-2,2]上恒成立,
在[-2,2]上恒成立,
当且仅当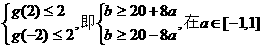 上恒成立。
上恒成立。
所以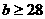 ,因此满足条件的b的取值范围是
,因此满足条件的b的取值范围是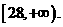 …………12分
…………12分
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分。
21.(本小题满分12分)
已知幂函数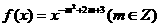 为偶函数,且在区间
为偶函数,且在区间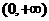 上是单调增函数。
上是单调增函数。
(I)求函数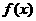 的解析式;
的解析式;
(II)设函数
(i)若函数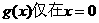 处有极值,求a的取值范围;
处有极值,求a的取值范围;
(ii)对于任意的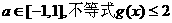 在[-2,2]上恒成立,求
在[-2,2]上恒成立,求 的取值范围。
的取值范围。
20.(本题满分12分)
(I)由
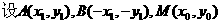
由A,M是椭圆上的点得,
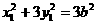 ①
①
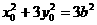 ②
②
①-②得,
 (定值) ………………5分
(定值) ………………5分
(II)点M的坐标为(0,1),则
显然直线AB的斜率存在,设直线AB的方程为 ,代入椭圆方程得,
,代入椭圆方程得,
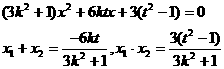
由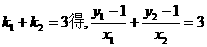 ③,
③,
又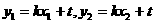 ④,
④,
由③,④得,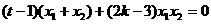 ,
,
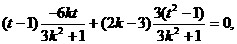
化简得,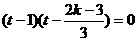
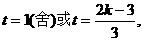 ………………9分
………………9分
则直线AB的方程为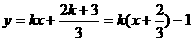
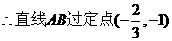 ………………10分
………………10分
20.(本小题满分12分)
已知点M是离心率是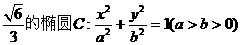 上一点,过点M作直线MA、MB交椭圆C于A,B两点,且斜率分别为
上一点,过点M作直线MA、MB交椭圆C于A,B两点,且斜率分别为
(I)若点A,B关于原点对称,求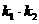 的值;
的值;
(II)若点M的坐标为(0,1),且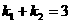 ,求证:直线AB过定点;并求直线AB的斜率k的取值范围。
,求证:直线AB过定点;并求直线AB的斜率k的取值范围。
3. 黑龙江四校一模
22. (本小题满分12分)
解 由题意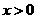 ,
,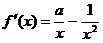 ……2分
……2分
(1)当 时,由
时,由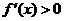 得
得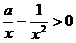 ,解得
,解得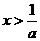 ,
,
即函数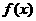 的单调增区间是
的单调增区间是 ;
;
由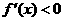 得
得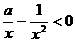 ,解得
,解得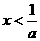 ,即函数
,即函数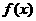 的单调减区间是
的单调减区间是
∴当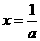 时,函数
时,函数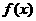 有极小值,
有极小值,
极小值为 ……5分
……5分
(2)当 时,∵对任意
时,∵对任意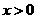 ,均有
,均有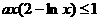 ,即有对任意
,即有对任意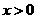 ,
,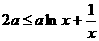 恒成立,
恒成立,
∴对任意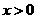 ,只须
,只须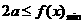
由(1)可知,函数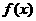 的极小值,即为最小值,∴
的极小值,即为最小值,∴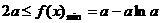 ,解得
,解得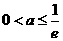
即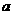 的取值范围为
的取值范围为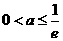 ……9分
……9分
(3)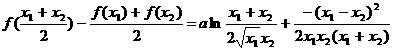
∵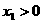 ,
,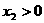 且
且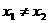 ,
,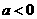 ,∴
,∴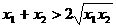 ,∴
,∴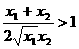 ,
,
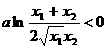 又
又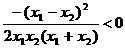 ,
,
∴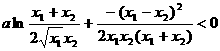
∴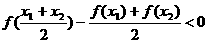 ,即
,即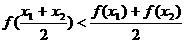 . ……12分
. ……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com